2019年10月24日上午南开大学经济学院云鹰读书会在经济学院圆阶205教室“国际经济与贸易科研训练：实证”课上顺利进行。本次读书会由国际经济贸易系2017级本科生吴本源展示Natalia Ramondo, Andrés Rodríguez-Clare, Milagro Saborío-Rodríguez的论文Trade, Domestic Frictions, and Scale Effects（2016），国经贸系王永进老师、徐楠老师、金威老师跟进并指导。

这篇论文的讲解主要分成5个部分：背景介绍，模型介绍，量化分析，与其他论文模型的一些讨论以及最终的结论。

第一部分：背景介绍

本篇论文主要讲述了如果将国家内各个地区间（例如中国的各个省份，美国的各个州）的贸易成本纳入考量的话，传统贸易模型（以EK模型为例）将会发生什么变化。作者主要是用287个“大都市”的数据(人口超过500000)，26个OECD国家之间的相互贸易额以及美国国内与国际贸易数据进行分析。得出的结论是如果将国内贸易成本纳入考虑的话，规模经济效应将会大大减弱，并且由模型得出的数据结果将会更契合真实世界的数据。

直觉上来说，我们所认知的传统贸易模型都指出，由于规模经济的存在，大国应该比小国富有得多。但是在真实世界的数据中，规模经济的程度却比我们想的小得多，是什么导致了这种现象呢？

一种观点认为小国能在开放的国际贸易中收益更多，事实确实是这样，但是这些贸易所得并不足以弥补和现实较小规模经济程度的差距。

另一种观点认为如果假设规模经济作用的对象不是国家的大小，而是整个世界。这样，由一个国家的大小引起的规模经济效应就被极大地弱化了，因为相对于世界整体而言，国家层面上的区别就非常微弱了。这也是解释现实世界中较小的规模经济的一个方向。

而在本文中，作者选取了另外一个渠道，即将国内的贸易成本纳入EK模型进行分析，并用实际数据进行量化计算，最终得到的结果与现实世界中的数据更加匹配。以上是本文的写作动机。

本文主要做出了抛砖引玉式的贡献，为之后国际贸易，尤其是关于国内经济地理，国家大小，开放程度，生产率相关的研究提供了一条更贴近现实的道路（将国内贸易成本纳入考量），并且提供了一个量化分析的方法。

第二部分：模型介绍

本文的模型主要基于EK模型，假设部分与EK中相同，唯一增加的就是考虑了国内的贸易运输成本。其中M与m代表地区层面，N与n代表国家层面。t代表科技参数，v代表工资水平，d代表贸易运输成本。图中列出了均衡的双边贸易流动量，价格指数以及劳动力市场出清条件。

以上两张图展示了当不存在国内贸易运输成本时国家层面的贸易额，价格指数，科技参数和效用水平（这里用实际工资表示）。由于这里假设不存在国内贸易运输成本，所以得到的结果与EK中得到的结果相似，这里的国家层面科技参数表现为国家内各地区科技参数按人口的加权平均。（详细的证明过程见附录）

接下来的假设一是一个关于人口与科技参数的假设，为了将之前的表达式化简，更易于分析。这里假设科技与人口线性相关，表现为人口乘以Φn,其中Φn表示该国家研发人员占比，以此表示该国家对于技术的重视程度。这个假设是由EK中生产效率的Fréchet分布推出的。根据Fréchet分布的特性，如果两个地区A与B的科技参数分别是t1与t2，那么这两个国家作为一个整体的生产效率就应该是max{A,B}。根据Fréchet分布函数的性质应将二者的分布函数相乘，整体的科技参数应为t1+t2，表现为二者的科技参数之和，这个假设也就应运而生。

根据这个假设，我们就可以用更简洁的方式表示出国家层面的科技参数以及改写效用（实际工资）表达式的形式，在这里我们可以看到Ln的指数为1/θ，这就代表着规模经济的作用。注意，到这里为止我们还未引入国内贸易运输成本，这里的规模经济就表现为传统贸易理论中高估的规模经济。我们将在之后的内容中讨论国内贸易运输成本对其造成的影响。

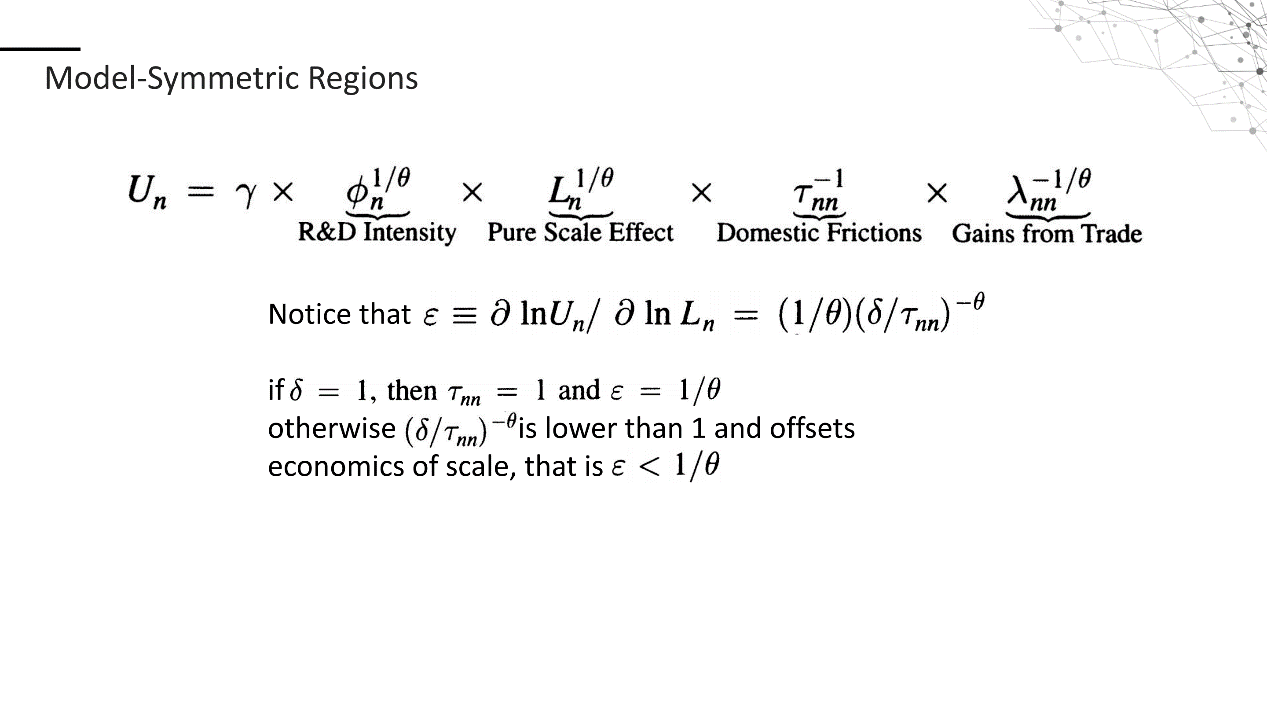
以上两张图中讨论了当存在国内贸易运输成本的时候模型将会有什么变化。假设二做出了一个地区间完全对称的假设，即假设每个地区的人口都相等，且任意属于两个不同国家的地区之间的贸易运输成本总是相等的。这样，在假设一和假设二的加持下，我们就可以计算出国内地区间的贸易运输成本为τnn。表现为选定任意一个锚点地区n，假设所有的国际贸易都视为从该地区进行，那么国际贸易的成本就表现为国际运输成本加上国内各地区运往n地区的成本。由于对称性的假设，每个地区都是相同的，那么除了作为本国1/Mn部分的n地区自己生产的产品不需要运输成本，d=1，其他（1-1/Mn）部分地区都需要σ的国内运输成本以运输到n地区（我们假设所有地区的成本都是σ以简化运算）。这样计算出来的Un就包含了4个部分，技术研发密集程度，人口引发的纯净的规模经济，国内贸易运输成本以及贸易所得（这一部分包含了国际运输成本）。注意到Un对Ln的弹性在存在国内贸易运输成本的时候是小于1/θ的，这就说明国内贸易运输成本的引入降低了规模经济的作用，与现实更加符合（证明过程见附录）。

除了上文分析的国内贸易运输成本的引入对规模经济效应的影响，我们还想分析其对进口比例，名义工资，价格水平的影响。为了计算这些影响，我们需要一个更强的假设，在原有假设的基础上，我们继续假设所有地区的技术开发密集度都是相同的，且所有国际与国内贸易运输成本都是相同的。结果发现，当τ＞σ时，更大的国家进口的份额更小，工资更高且价格水平更低，而当τ=σ时，更大的国家进口份额仍然更小，但是工资水平和价格水平在各个国家间没有差别。另外，在τ＞σ时实际工资随着国家变大而上升，这是由于更高的工资和更低的价格引起的，但是当τ=σ时，这样的规模经济将不复存在，这也告诉我们国内贸易运输成本的引入削弱了规模经济的作用。（证明见附录）

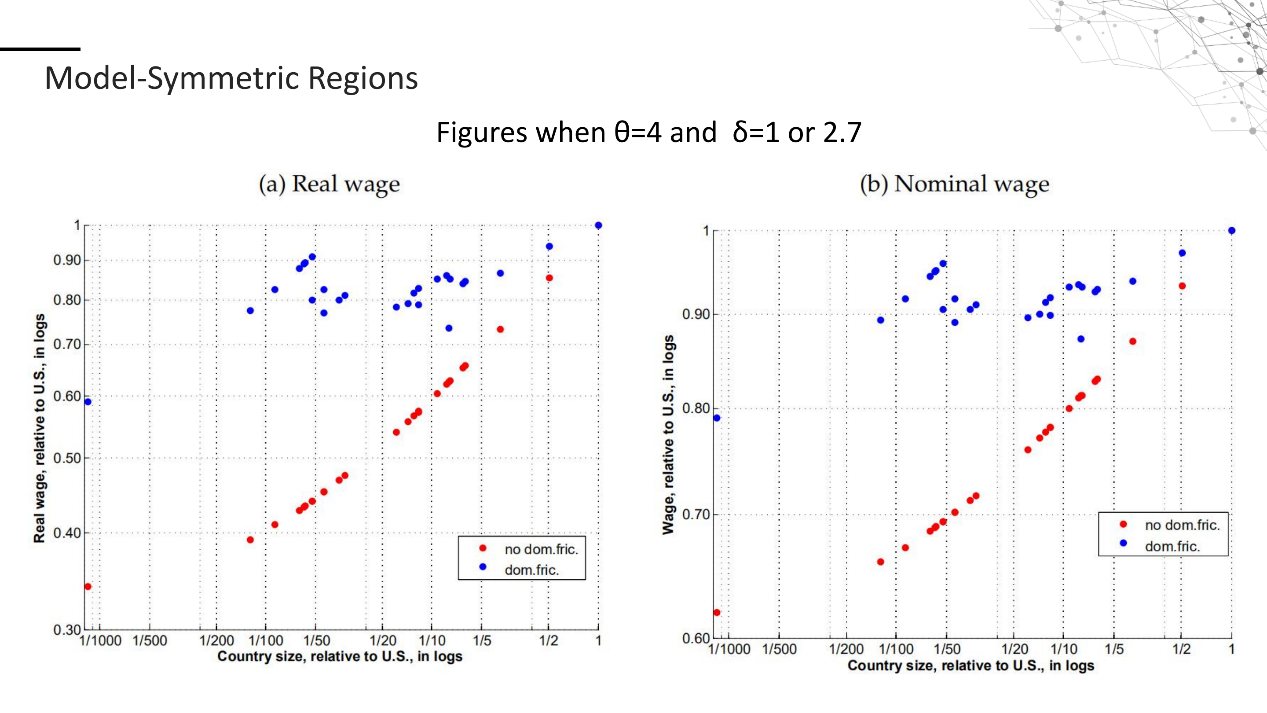
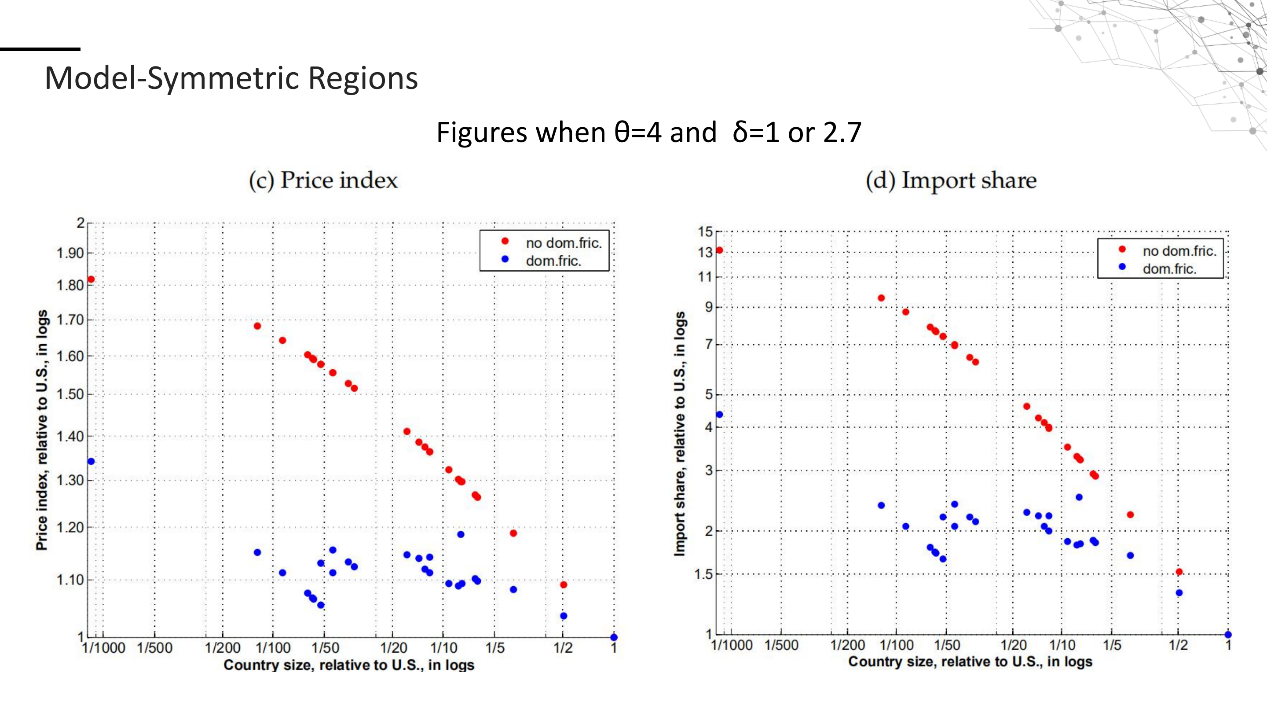
以上四张图表现了不存在国内贸易运输成本（红点）和存在国内贸易运输成本（蓝点）规模经济在名义和实际工资，价格水平，进口份额上的表现。可以看出在这四张图中，引入国内贸易运输成本使弹性大大降低，也就是使得规模经济程度大大降低，更加符合现实世界的情况。

第三部分：量化分析

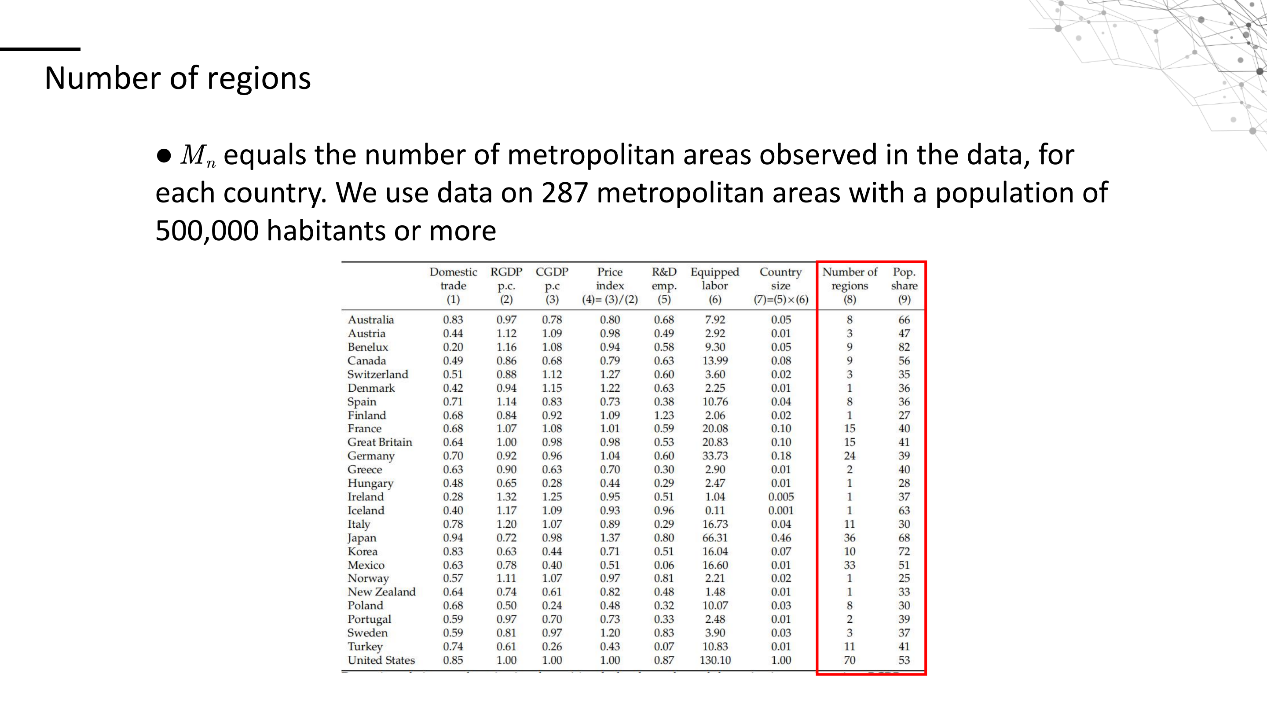
作者主要使用26个OCED国家的数据，为了量化分析该模型，我们需要得出弹性θ，各个国家的地区数Mn和技术研发密集度Φn，每个地区的人口lm，以及最重要的，各个地区间的贸易运输成本矩阵dmk

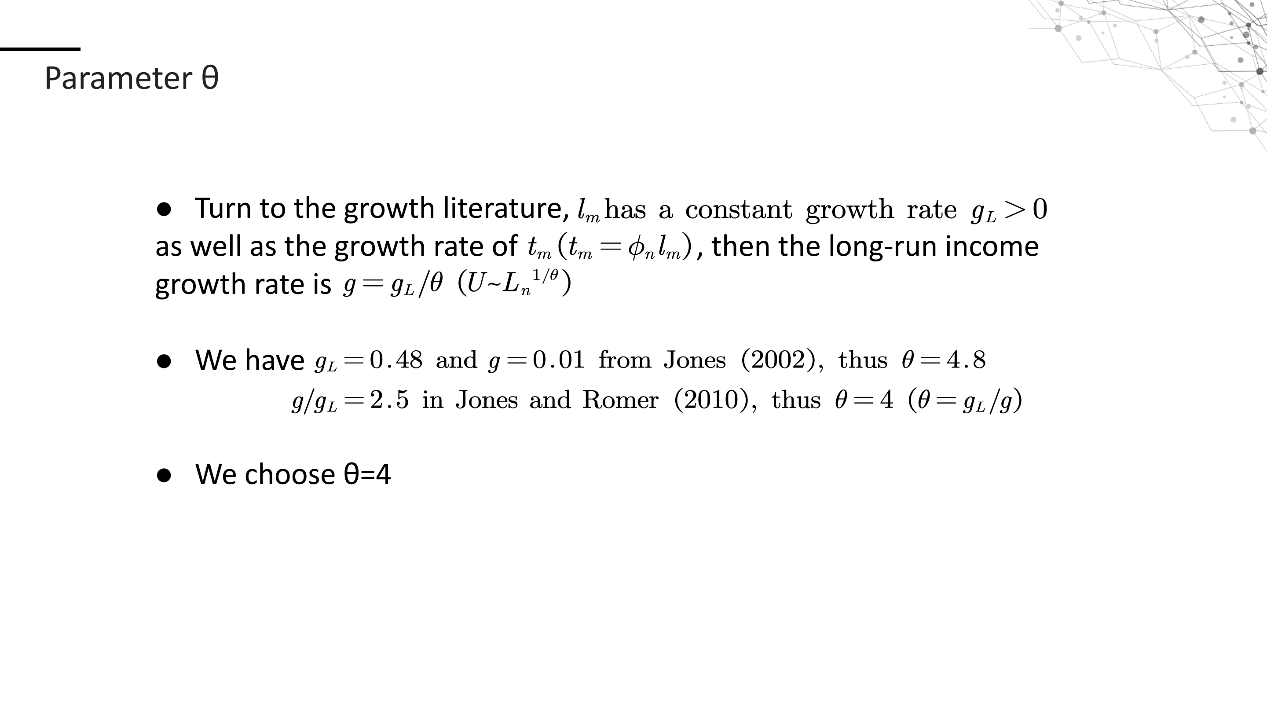
作者选取了Jones和Romer文献中给出的θ=4，用大于500000人口数量的大城市作为地区的数量Mn，R&D研发雇员占比作为技术研发密集度Φn，具体数据见文中表格所示。

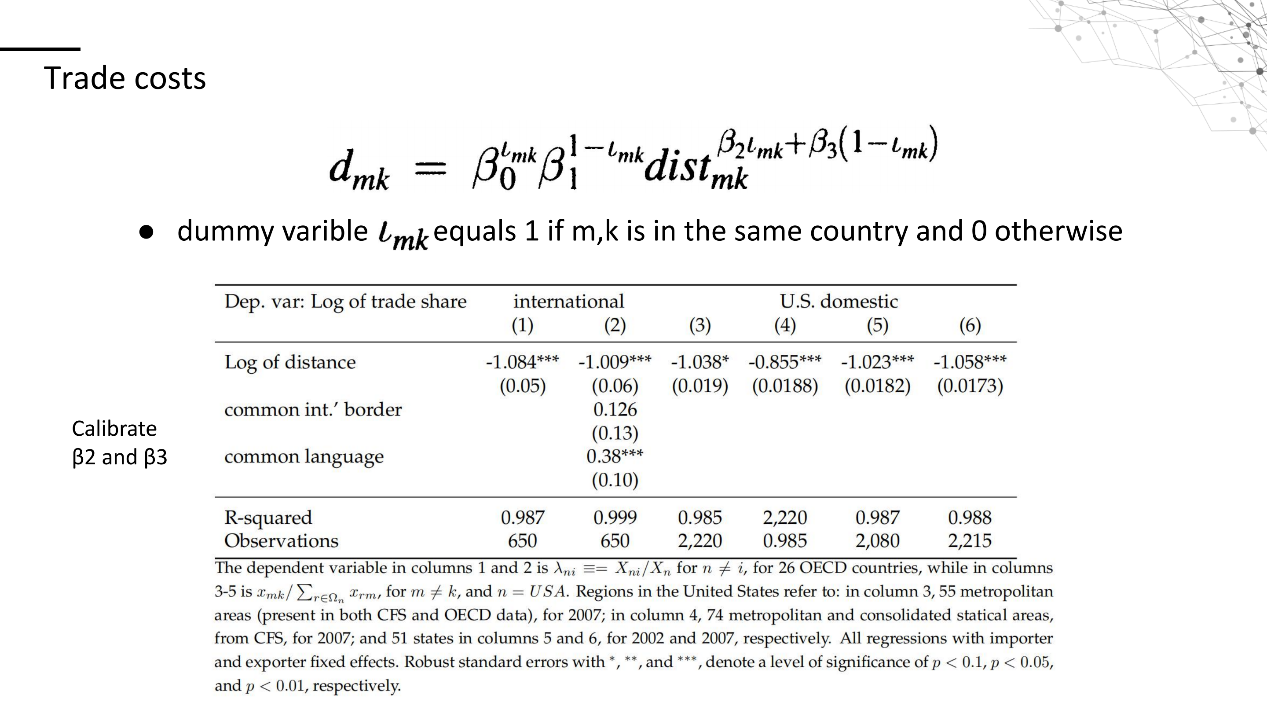
由于得到每个地区之间具体的贸易运输成本矩阵显然是不可能的，这里作者给出了一个估计式，运用OLS方法，使用美国内部贸易的数据，以及相关文献中的结果，估计出β2=β3=βdisc=0.27，同时β0=2.33，β1=2.89，具体的估计过程详见文中的表格。

在得到以上所有参数之后，我们就可以对每个国家进行量化的计算，计算结果显示该模型得出的数据与现实世界真实的贸易模式吻合度很高，具体地说，96%的双边国际贸易份额都被我们模型得出的数据观测到了。对于国家层面的进口份额来说，模型计算出的数据和实际的数据有0.8的相关系数，出口份额有0.65的相关系数。尤其是加拿大的国内贸易比重，模型计算出的是0.77而现实数据是0.77，非常接近，从中可以看出文中的模型计算出的结果是相当不错的。

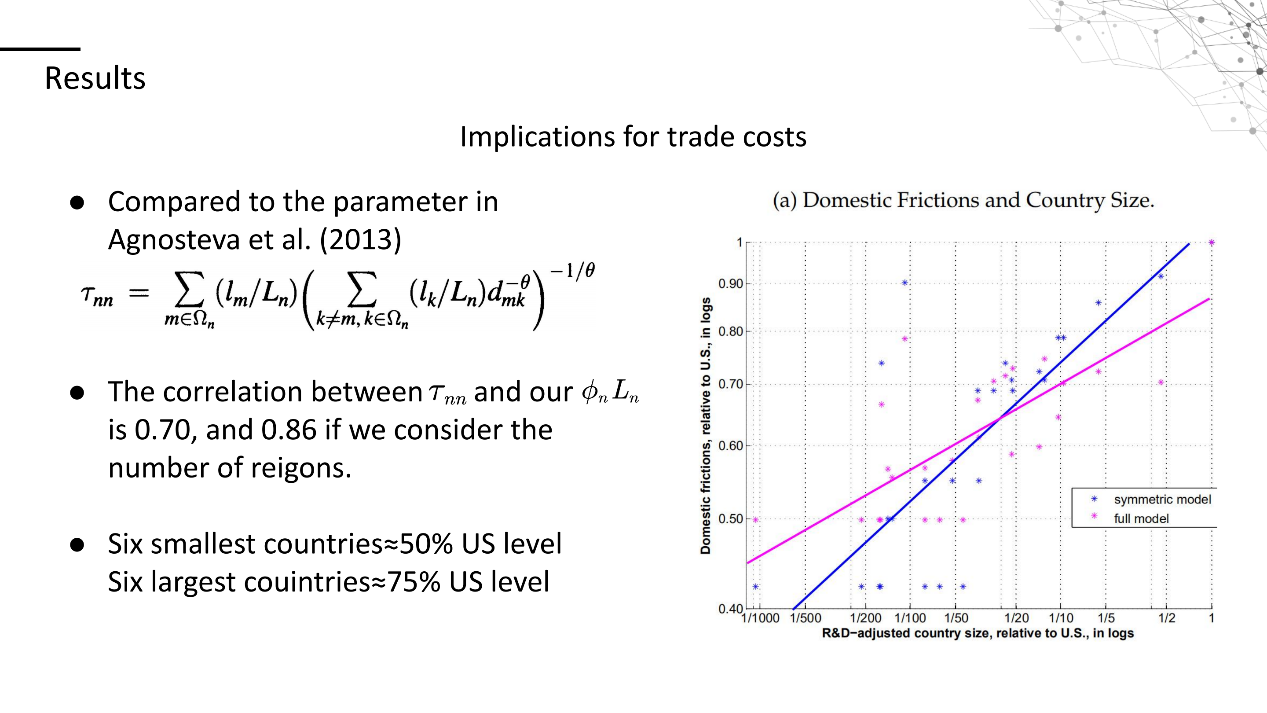
接下来我们要将我们得出的结果中国内贸易运输成本的部分与现实世界的数据相比较，作者选取了Agnosteva et al. (2013)中给出的衡量国内贸易运输成本的指数（紫色）与模型中计算出的值（蓝色）进行比较。可以看出两条线较为接近。同时也可以发现，国内贸易运输成本与ΦnLn呈现显著的正相关关系，相关系数为0.7(考虑地区数量后是0.86)。这就说明国内贸易运输成本与国家大小密切相关。举例来说，一个很小的国家，例如丹麦，国内贸易运输成本几乎只有美国的一半，而较大一些的国家例如日本国内贸易运输成本大概是美国的70%。在我们选取的国家中最小的6个国家的国内贸易运输成本大概是美国的一半，最大的6个国家的国内贸易运输成本大概是美国的75%。都说明国内贸易运输成本的引入会以这种方式削弱规模经济的作用。

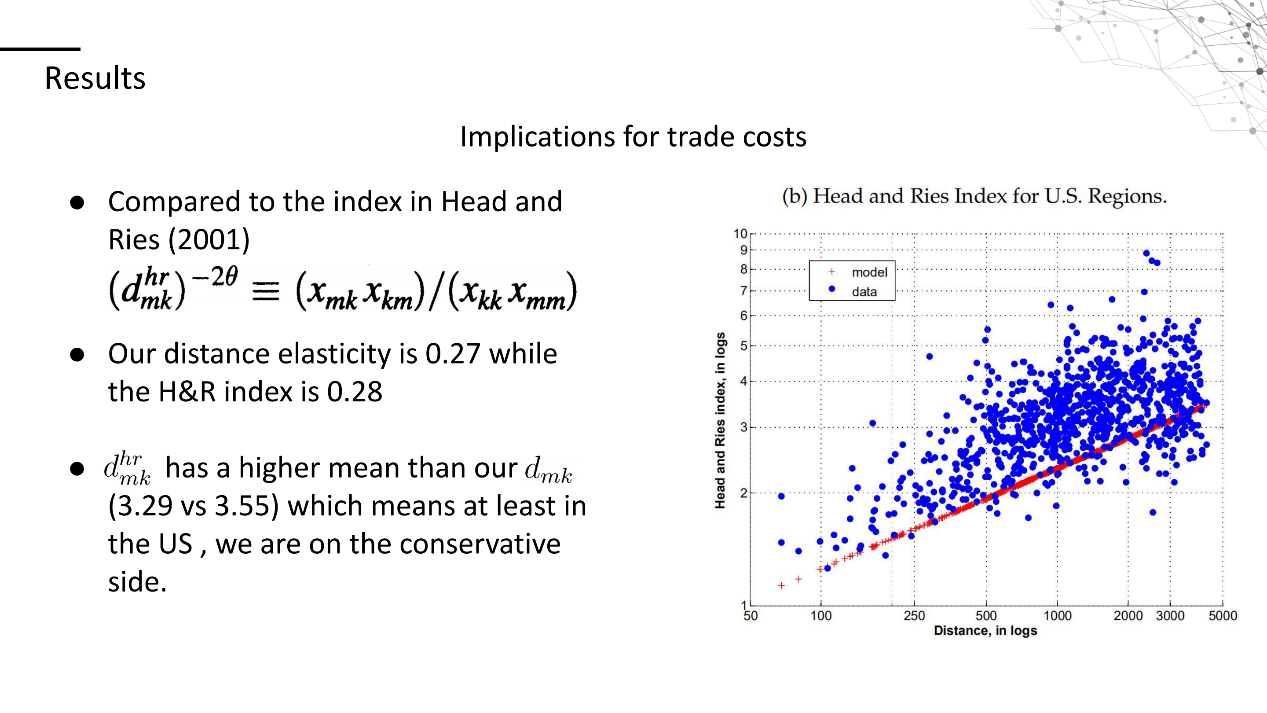
接下来，作者又选取了Head and Ries (2001)中描绘地区间贸易运输成本的指数（蓝点）与本文模型计算出的数据（红点）相比较，得出本文相对距离的弹性为0.27，而H&R指数中的是0.28，非常接近。同时，本文中的均值更低，说明我们对于地区间贸易运输成本的估计是保守估计，实际的地区间贸易运输成本可能比我们的估计的还要大，对于规模经济的影响也可能更大。

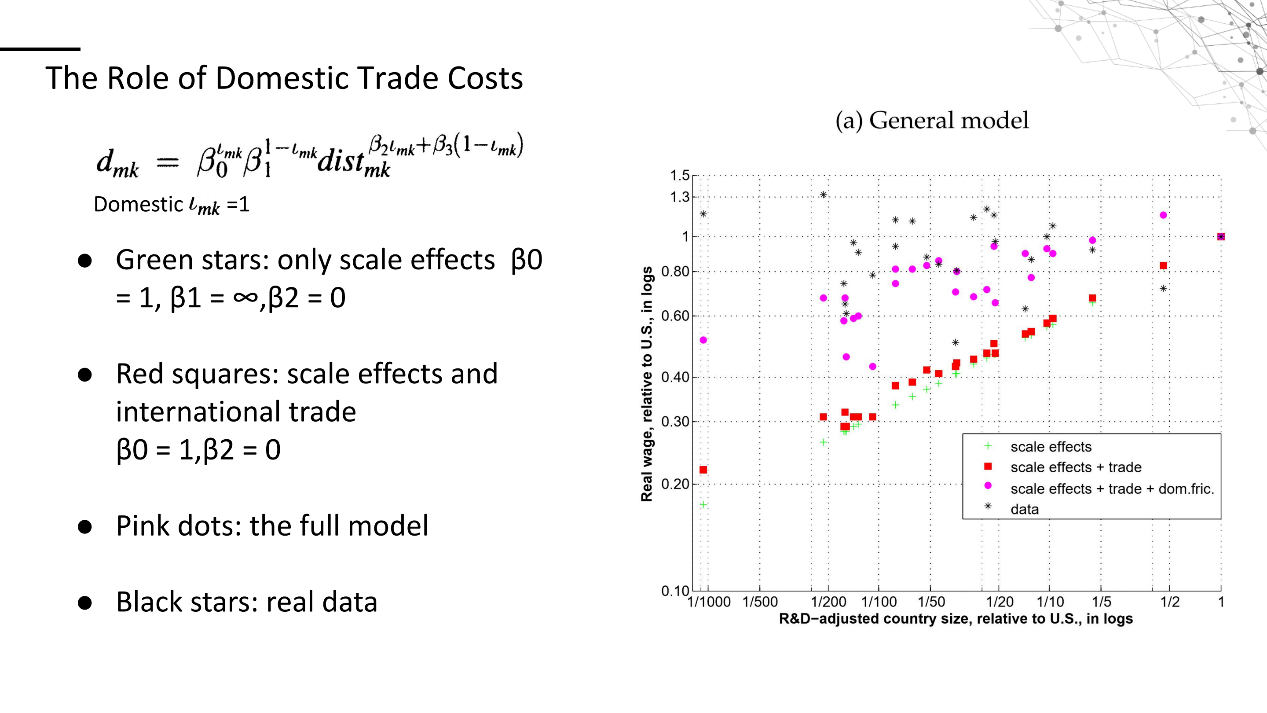
紧接着我们研究到底国内间贸易运输成本的引入会对规模经济造成多少影响。在之前的估计是中，通过改变不同的β0，β1和β2的值，我们可以计算出仅有规模经济效应的值（绿点），包含规模经济效应和开放国际贸易的值（红点），包含规模经济效应和开放国际贸易以及加入国内间贸易运输成本，也就是我们模型给出的值（粉点），以及真实数据（黑点）。将它们作图比较。

可以发现不存在国内贸易运输成本的红点和绿点与真实数据黑点相差很多，尤其是对小国来说差距相当大。这就说明相比于仅有规模经济效应的绿点，加入国际贸易的红点并没有使其与真实数据的差距缩小很多，即使小国的确从开放的国际贸易中获益更多，但那还远远不够。相比之下，加入了国内间贸易运输成本的粉点与真实数据黑点就接近的多。但也并不是完全高度重合，仍然存在误差和其他可能存在的因素。对于名义和实际工资，价格指数和进口份额来说结论都是一样。具体可以参考文中的图像。

第四部分：其他论文模型的一些讨论

我们在文中讨论的都是基于对称性假设的模型，这里讨论当贸易运输成本并不是对称的时候将会发生什么，主要用本文的模型与EK(2007)和Waugh(2010)中的模型进行比较讨论。

由于EK模型是进口侧导致的贸易运输成本不对称而Waugh模型是出口侧导致的贸易运输成本不对称，且EK和Waugh中都不存在同一国家不同地区之间的贸易运输成本。于是我们可以把EK与W模型中的地区间贸易运输成本表示出来，如上图所示，与本文模型不同的是乘上了一个代表不对称性的在进口或出口侧的参数。

结果表明本文和W模型中的工资和贸易额都是相同的，但是与EK中不同。特别的是，在W模型中，更大的国家并不会更富有，因为W模型中的技术也是有传播成本的，这个传播成本会随着国家的变大而变大，就像本文中的τnn一样。

现实世界中许多产品的生产都需要中间产品，并且也存在一些不可贸易的最终产品。接下来我们讨论当存在中间产品和不可贸易产品时的情形。用g代表中间产品，f代表最终产品，η代表中间品所占的比重。这样就可以将之前得到的效用水平（实际工资水平）改写成包含中间产品和最终产品两部分的式子以便进行下一步的讨论。

假设没有地区间的贸易运输成本，并且最终产品在国家间是无法贸易的。这样效用水平的方差又可以进一步改写，如上如所示。注意到改写之后的方程中λnn，即贸易所得的指数从     1/θ降低到η/θ。说明如果最终产品无法贸易，规模经济保持不变但是贸易所得将减少。

再假设如果最终产品在地区之间也是无法贸易的，也就是说δn为正无穷，阻断地区间的贸易，这样可以进一步改写Un，此时可以看出规模经济的指数从1/θ降低至了η/θ，即如果最终商品在一国的地区间无法贸易的话，会降低规模经济的作用。

再考虑另外一种情况，如果技术在各个地区，各个国家之间是可以传播的，并且假设传播不需要成本。这样，我们又可以进一步改写Un，可以看到改写之后规模经济作用的对象是ΣL而不是之前单独的L，即规模经济作用于整个世界，而不是一个国家。这样的话相当于大大减小了规模经济的作用。

第五部分：结论

本文的核心结论就是将地区间贸易成本纳入传统贸易模型的考量，可以使模型得出的数据更贴近于现实世界中的TFP水平，进口份额，实际工资与相对工资，以及价格水平。作者给出了这样一个改进模型的思路和量化分析的过程，为之后研究相关方向的研究者们做出了抛砖引玉的贡献。

下期云鹰读书会将于2019年10月31日上午,在南开大学经济学院圆阶205教室举行。下一篇论文是Fan, Tang,Zhu and Zou,2018, The Alibaba Effect: Spatial Consumption Inequality and the Welfare Gains from e-Commerce,Journal of International Economics

敬请期待！

稿件来源：吴本源

编辑：石惠芳，杨瑛凡

审校：王永进