2019年12月19日上午，南开大学经济学院云鹰读书会在经济学院圆阶205教室“国际经济与贸易科研训练：实证”课上顺利进行。本次读书会由国际经济贸易系2017级本科生王一凡展示Jae Wook Jung; Ina Simonovska; Ariel Weinberger的论文Exporter heterogeneity and price discrimination: A quantitative view，国经贸王永进老师、金威老师跟进指导。

Contribution

在本文中建立了一个一般均衡模型GCES model，这个模型将企业异质性，非位似偏好相结合，并且使用了类似于CES效用的函数，引入了商品的替代弹性。这个理论框架满足了企业间的价格差异和市场间的价格差异的设定，同时可以比较好的拟合企业的销售额和价格加成分布。总之，GCES模型是一个比较合理，在拟合数据方面更具有优越性的分析模型，可以通过GCES模型来进一步精确的量化贸易福利。

本文分为Introduction、Generalized CES Model、Solution Algorithm、Existing Variable Markup Models、Quantitative Analysis、Conclusion六部分。

1.Introduction

在现有的国际贸易文献里面，有一些异质性企业在定价与商品流动方面发挥重要作用的典型事实:

1. 出口商仅占企业的一小部分

2. 享有高生产率和规模优势高生产率的企业可以获取更高的价格加成

3. 出口商在更富裕的国家可以有更高的价格加成

在企业的规模分布上也存在着帕累托分布现象，帕累托分布一般是指百分之二十的人享有百分之八十的财富，一小部分在整体中起关键作用，套到国际贸易的企业上面，只有小部分的企业占据了绝大部分的生产和销售份额，这些大规模企业起着相当大的作用，大部分企业都是小企业。

本文的重点就在于所建立的GCES模型可以同时满足上面这些典型事实，比现有的相关模型更加优越精准，可以更好的符合现实并拟合数据，量化贸易福利的结果也更加准确。由于GCES模型在微观和宏观数据上都表现得很好，那么有理由认为GCES作为一个衡量贸易福利的定量分析框架更加具有可信度。

在本文中也将其他三种模型与GCES进行了对比，进一步证明了本文GCES模型的优越性。Melitz and Ottaviano (2008) (MO), Behrens et al. (2014) (BMMS), Simonovska (2015) (SIM)，这三个模型和GCES的效用函数不一样，但供给侧的结构一样，MO&BNNS&SIM在企业的截止成本上得到了与GCES类似的结果。但是，在同时满足销售额和价格加成分布方面，这些模型都不如GCES模型，所以GCES是更好的模型。

为什么我们选择销售额和价格加成分布作为模型分析的两个关键条件?原因在于，在一些相关贸易实证文献中，这两个分布是定量分析的核心部分，第二，这两个分布的统一现在还难以找到，CES框架对于销售额的分布很有效，但无法产生价格歧视。所以我们试图把这两者结合，构造另一个仿CES的效用函数。最后，根据ACDR，这两个分布又与福利测算的关键参数相关，通过着两个分布更精确地量化贸易福利。

2.理论框架

2.1 framework

企业生产差异化的产品

I：世界上参与贸易的国家总数

i：出口国    j：进口国

Gi() = 1−(bi/φ)θ：i国的企业所面临的生产率的分布

φ：生产率，φ∈[bi，） bi：一个国家的一般生产水平。

Wi：i国居民的工资，即i国的人均收入

L：生产中使用的劳动力数目

x=φL：产出等于生产率乘劳动力

τ：从i国运输到j国的一个运输成本

 i国企业生产一个商品再运输到j国的一个边际成本。

μ：出口成本为c的时候i国企业能出口到j国的比例，

        出口的临界成本，它代表企业以最低生产率bi出口j国的成本

于是

2.2 Consumer and Firm Problems

根据CES构造消费者效用函数，得到

        一个国家特定变量，引用了之前一个文献的结果。>0则需求价格弹性不随销售额的增加而增加，即使一个企业的生产规模再大，由于弹性不会增加，人们对于产品价格不敏感，这个企业不必因为销量大而降低价格，符合之前生产率高的企业可以享受更高的价格加成的事实。

在此效用函数中，消费者消费一种产品所获得的效用是有限的，消费者会在价格高到一定程度时选择不消费这种商品。继而产生choke price，使消费者需求为0时的价格就被称为窒息价格。

根据上述效用的最大化，可以仿照CES需求的求解去推导出需求函数，需求函数乘上消费者的数量就是i国企业出口到j国时面对的总需求。为总体价格指数。

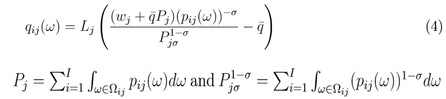
在得到企业面对的需求之后，根据企业利润最大化（eq5）求一阶导数为0可以得到最优价格（eq7）：

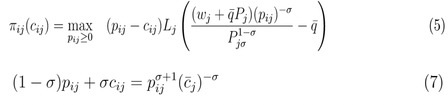
将i国企业出口所有目的地获得利润加总，得到i国一个企业的总利润：

        识别一个企业从i出口到j的临界成本：在处于临界成本时，企业即使以最低价也就是成本价销售，也只能得到0需求。即

时，需求为0。而对于j国市场而言，来自任何一个国家的产品需求为0时的价格应该都是一样的，在j国市场上，有一个统一的截止成本。

企业供给x等于消费者需求，企业销售额r等于价格与产出的乘积：

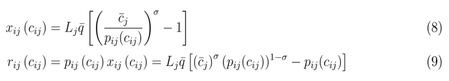
根据eq7，dpij/dcij > 0，即随着成本增加价格也会增加。但是价格上升的比例要小于成本上升的比例，为了进一步说明这一点，我们定义价格加成，mij = pij/cij，将eq(7)用m改写得到dmij/dcij < 0，即随着成本的上升，价格加成会减少，成本的上升并不会完全反映到价格上面去，从成本到价格上存在这样一个传导通道passthrough，传导通道是不完全的，并不会把所有的成本上升反映到价格上面去。

在GCES里面m∈[1,σ/(σ − 1)]，一个企业不能收取无限的价格加成。根据eq9，如果企业出口的市场足够大，企业就可以有无限的销售额，销售额来源于价格和数量，在企业价格加成有限时，无限的销售额就来自于数量，企业生产数量等于劳动力数量乘生产率，而企业生产率已经在进入市场时确定下来，就只能依靠增加雇佣的劳动力。因此需要无穷的劳动力，才能生产无穷的产品，这会使工资无限上升，也就是说，没有企业能够达到这个结果。但是在σ=1的时候，企业不需要无穷的劳动力也可以达到这种效果，就可以有无限的销售额。在这种情况下出口商与非出口商之间的差异就会被过高估计，不能很好地拟合数据。这也是GCES模型更符合现实的一点。

2.3 Equilibrium

将之前的表达式统一成关于成本的式子，方便后面的运算解出整个模型。下面分别为i国一个企业的期望利润（eq11）、i国出口到j国的贸易额（eq12）、j国价格指数（eq13、eq14）。

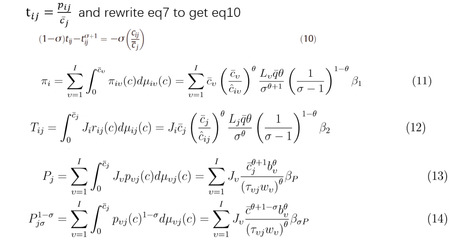
自由进出条件：沉没成本等于利润，企业获得零利润。收支相抵条件：i国所有居民的总收入，等于i国与世界各国以及本国在内的贸易额，即i国居民的总花费。根据企业的自由进出和收支相抵得到eq15、eq16，解出i国企业数量Ji = βJLi/fe, βJ是一个常数。

λ：贸易份额，i国出口到j国贸易额占j国市场的比例。Eq16、17相结合得到Eq18，左边是i国居民的所有收入，右边的求和符号里面是j国居民的收入花费在i国产品上的部分，也就是Tij，i国出口到j国的贸易额，在把所有的j国加起来，就是i国总出口以及在本国市场上消费的部分，等于i国居民总收入。由此解出i国工资。

2.4 Model predictions

2.4.1 Sales distribution

首先是销售额的分布，将销售额r改写成关于产量x的式子，当x趋于无穷时，销售额与产量成正比，而产量等于生产率乘劳动力，也就是当产量趋于无穷时，销售额可以看作是生产力的单调变换。因此，当生产率是帕累托分布(Mrazova et al. (2015)) ，销售额的分布将是帕累托的分布。

2.4.2 Distribution of markups

将价格加成m标准化，即用单个企业的价格加成除以i国企业在j国市场上的价格加成的平均值

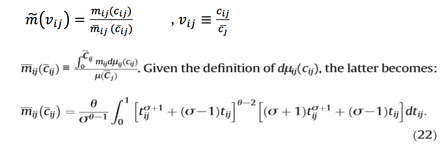
由于价格加成是关于成本的单调减函数，企业的价格加成≥的概率等于企业的成本≤所对应的成本的概率，进而得到价格加成的分布

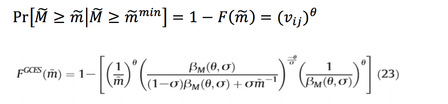
2.4.3 Pass-through elasticity

根据最优价格表达式改写成价格加成的形式，得到m关于成本的隐函数，由此可以求得一个企业的价格加成弹性，再将一个国家里市场上所有企业的价格加成成本弹性按企业占据市场份额加权得到总的价格加成成本弹性（eq39）

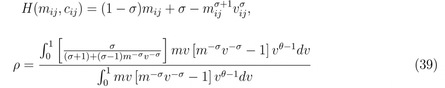
         2.4.4 Income per capita and prices

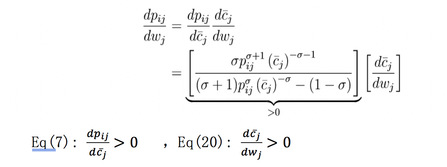
GCES模型符合现实中可贸易商品在更富裕的地方价格更高一些的情况，即这种可变的价格加成模型对于大部分同质商品在不同地方价格差异的原因有解释力度。

2.5 Discussion

上述预测表示GCES模型与企业异质性的现实表现是比较相符的，我们的模型也可以产生随着公司规模、不完全传递的存在以及基于消费者收入的公司价格歧视而增加的价格加成。同时，根据ACDR，这些东西（生产力的集中、销售额的分布、成本传递到价格的通道）对于量化贸易福利是很有必要的。

3.Existing non-homothetic models

为了评估GCES模型的贡献，将其与其他的企业异质性、非位似偏好模型进行比较（SIM、MO、BMMS）。

首先按照之前的GCES模型推导这些模型的销售额和价格加成分布，推导过程和第二部分的推导一样，只是效用函数有所不同。以下分别为SIM、MO、BMMS效用函数

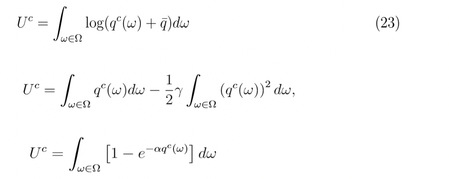
将销售额和价格加成标准化，再求得三个模型的销售额和价格加成分布

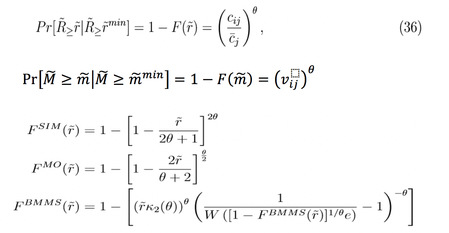
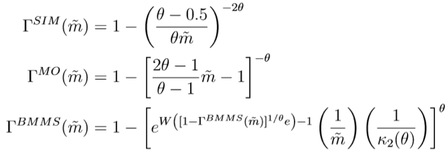
在推导出这些模型的销售额和价格加成分布之后，可以看到，一个模型的两个分布同时取决于一个参数。一个参数值难以同时拟合事实中的销售额和价格加成分布。用销售额的数据可以估计一个拟合销售额的分布，也用价格加成的数据估计出另一个，这两个相等的可能性是非常小的。这就是作者所说的这些现存模型的缺陷。而GCES模型模仿CES函数构造效用，引入了σ，就可以利用σ和去配合同时拟合两个分布。

4．Solution Algorithm

本部分介绍了求解算法，对 GCES 模型进行了定量分析。我们使用智利的企业数据来匹配企业的销售额和价格加成分布。为了估计我们需要的参数，用模型再现企业的销售额和价格加成分布，我们需要非常大的数据，因为模型中假设企业是连续的，而事实上企业是离散的，必须足够多的数据点组合在一起才能接近连续的状态。因此整个运算过程在理论上非常繁琐。

选择300万个firm，均匀分布在0-1，效用为0-1，把效用按增序排列，找到最大的效用，Umax。定义s等于效用除以最大效用，本国的产品边际成本为cii=s^(1/θ)*ciba。知道了在本国的生产成本之后，只需找到合适的运输成本，我们就可以让企业出口到不同的国家了。

 4.1 From model to data

目前需要知道的参数值有，θ，σ，人口，运输成本，各国的工资和各国的cutoff截止成本。（人口、工资和cost cutoff都需要除以一个计价国家的人口、工资和成本，来进行标准化）

根据2010年waugh的文献，为双边贸易成本设定了一个函数形式，α是常数，exi是出口商固定效应，dh是判断贸易是否是跨国贸易的一个指标，dist是贸易的这一组国家之间的距离，tij是国家间的时区差异，cepii是包含与这组国家特征的一些指标的矩阵。然后利用贸易数据直接估计这些系数。我们将交易费用的函数形式替换为引力方程，取对数，通过 OLS 估计系数，从而得到了双边贸易成本τ。

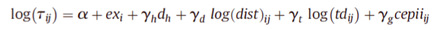
利用eq10λij除以λjj再取对数得到下式，φ表示国家固定效应。（将贸易成本除以在销售的国内同行的成本进行标准化使国内贸易成本为1）。我们可以利用现有的贸易数据直接得到真实的贸易份额、估计出国家固定效应，再将关于贸易成本的引力方程代入，那么，在给定θ的情况下，就可以估计出贸易成本引力方程里面的系数。

根据eq20，可以得到eq29，也就是说，估计出智利的截止成本之后，只需要工资、人口、国家固定效应求出eq29的值，不需要利用j国企业数据再去拟合分布就可以直接得到j国的截止成本。

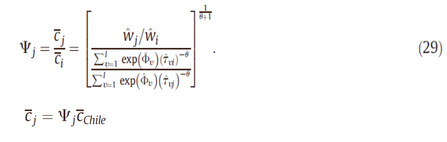
接下来就是估计本模型中的两个关键参数θ和σ。采用两种方法去估计：恰好识别和过度识别。前者是指方程个数等于被估参数个数，后者是指方程个数大于被估参数个数。

恰好识别需要两个方程，我们使用智利的测量的销售额优势等于真实数据的销售额优势，以及智利的测量的价格加成优势等于真实数据的价格加成优势。

智利出口商对非出口商的价格加成优势，来自于二者的价格加成的对数形式相减（为简化运算取对数）。

由于没有中间投入品，生产的附加值就等于劳动的价值就等于企业的总收入。δ是识别企业是否进行国际贸易的一个虚拟变量，va是一个企业生产的总附加值。该企业雇佣的劳动力数目emp，c是生产一单位产品的成本，企业将x单位产品运输到v需要生产τx单位产品，除以劳动者的工资，就得到了劳动力数量。利用二者相除得到生产率，即单位劳动者产出的价值，同时价格加成等于产出值除以成本（工资），由于一个国家内部劳动力工资相等，所以在衡量出口商与非出口商优势时，为简化运算仅使用生产率表示价格加成。

接下来就是识别出口商与非出口商进而计算二者之间的价格加成差异。我们要靠他们的成本来区分企业是否能出口。引入了ciix，企业出口到最近的目的地的截止成本，也是企业出口的临界成本。如果企业成本高于此，只能在国内销售。只有低于该成本的企业才能至少出口一个国家，成为出口企业。利用eq10，令j=i来计算这一成本界限，进而得到区分i国市场的出口企业与非出口企业的成本所对应的t值。将所有非出口企业的测量的生产力取积分，就得到非出口商的平均优势。

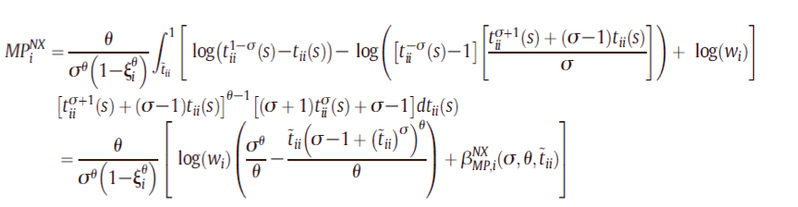
为了减轻计算负担，我们希望将出口企业出口v国计算生产率优势时用到的tiv转化成tii，这样可以将对v出口时的计算也用tii积分，所以需要找到tii和tiv的关系。在得到上述关系之后，继续对出口商的生产率积分，得到出口商的平均生产率。用出口商的平均生产率减去非出口商的，就得到生产率优势。

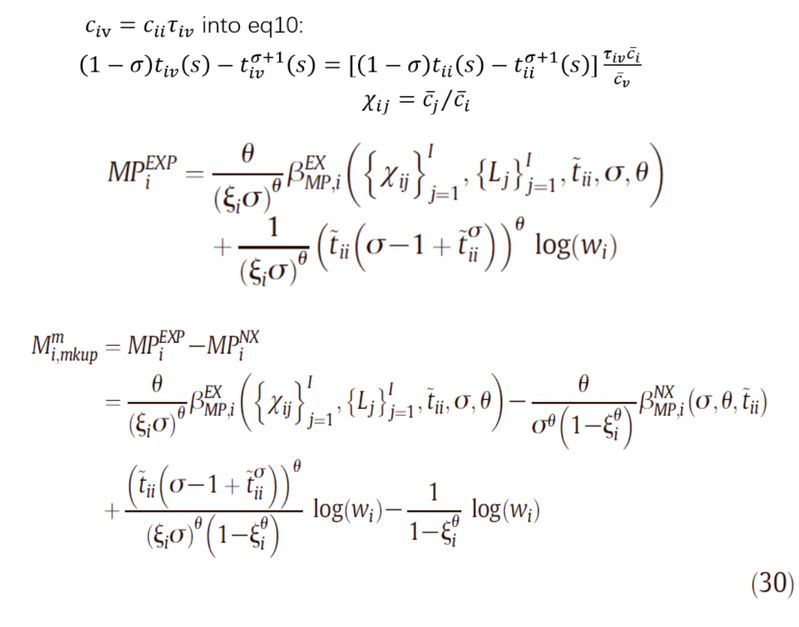
销售额优势是估参时用到的第二个关系。就使用出口商的平均国内销售额与非出口商的平均国内销售额的比值即可，将之前求到的企业销售额r的表达式对t进行积分即可得到。

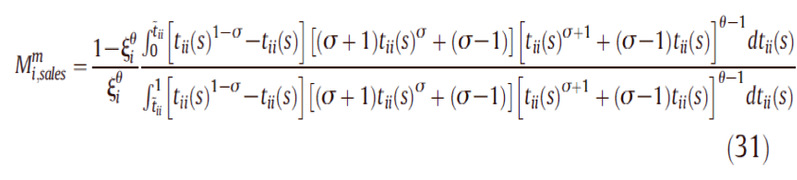
估参时使用了两个方法：恰好识别和过度识别，二者在于被估参数个数和方程个数的不同。在恰好识别中，估计两个参数，用下面这两个矩

在过度识别中，加入了销售额和价格加成的具体的分布的情况的估计，在每个分布中加入了三个百分比，比如说，我们模型模拟出来的占90-99百分位的销售额的企业比例尽可能等于数据中的占据90-99百分位的企业比例，还有90-10和90-50，同样的操作也在价格加成中进行，这样就有了六个等式来估计两个参数。

4.2 Alternative identification: trade elasticity

GCES使用企业分布的矩来估计贸易弹性θ。 这种做法的缺点是贸易弹性的估计可能与文献中的标准估计大相径庭，这将导致θ估计值不同，进而导致大不相同的福利收益估计。

基于这个原因，我们考虑一种替代性的识别策略，这更符合现有文献的估参方法，即利用价格变化来估计引力框架内的交易弹性，但遵循前一小节描述的结构估计策略。在这个识别策略里面，不再使用之前所用的销售额和价格加成分布去估计θ，采用了更符合其他模型估计贸易弹性时所使用的条件去估计参数，但是模型的基本框架结构还是GCES模型。

选择了三个矩去估计θ：首先是最大价格差异，在模型中模拟的企业会出口一种普通产品向其他国家，企业间生产的产品是异质的，但是企业自己出口向不同目的地的产品是同质的，我们使用了66个国家的价格数据来体现价格差异，就在企业同时向这66个国家出口的同质产品中随机挑选110种商品，记录这一百一十种商品在不同国家的价格组成价格矩阵，来构建最大的价格差距；第二个关系就是，位于第八十五百分位的价格差距；第三个关系是，最大价格差距和两个目的地之间的相对人均收入的协方差，之前我们成功估计出来不同国家的工资，也模拟得到了最大价格差异，就可以去构建二者的协方差。

使用过度估计方法，用以上三个矩在固定σ值的情况下，估计sita。

5.Quantitative Results

5.1 data

企业层面：采用智利的企业数据，由智利全国工业调查局提供、国家统计局收集，每年大约有5000个公司级别的样本数，因为我们对企业的截面数据感兴趣，将样本限制在2004年。这个数据库里企业层面的数据非常详尽， 每家公司都提供详细的经济数据，如总销售额、员工人数、工资、固定资产价值、中间投入支出等。重要的是，公司也报告他们作为出口的总销售额，因此我们可以为每个公司构建国内销售额，也可以利用增值和劳动报酬来计算价格加成。

贸易层面：首先是模型中使用的贸易份额是2004年66个国家的贸易份额的数据，来自UNIDO数据库，我们在计算λ时对其进行了调整，用贸易量除以本国实际消费的总产出，也就是减去出口加上进口。其次是来自cepii的关于不同的国家组合的引力变量的数据，也就是我们前面用到的估计贸易成本时用到的矩阵。最后是来自penn world table8.0的人口数据。

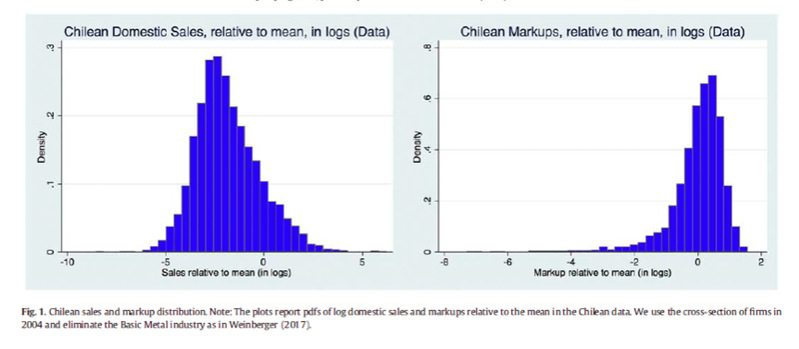
通过智利的企业数据直接得到其销售额分布和价格加成分布，以方便之后和用模型得到的两个分布去进行对比。下面两幅图就是2004智利企业的两个概率密度分布，左边是销售额分布，右边是价格加成分布。两个分布均表示原数据标准化再取对数得到结果的分布情况，横坐标的0表示销售额等于平均销售额，左边就是小于平均销售额的部分，右边就是大于的部分，另一幅价格加成的图也是这样。

在第一张图中，超过平均销售额的公司的比例，也就是在0右侧的面积只占整个分布的一小部分，也就是说只有相对较小比例的企业拥有着更高的销售额，这和我们使用的帕累托分布的一般概念：20%的人占有80%的资源相一致。而第二幅图显示出价格加成明显的左偏分布，左半部分的尾部这和我们模型无法产生这种尾部，但可以与右边的尾部分布情况相吻合，我们的模型右边和图中一样也呈现出一种厚尾特征，获取高水平的价格加成的企业的比例也是有限的

5.2 Estimates

GCES模型定量分析的结果证明了我们使σ＞1的假设非常有效的拟合了数据，销售额和价格加成的分布可以同时比较有效的拟合。σ影响的是产品之间的替代性，进一步影响生产率高的企业的规模。就是说，如果产品替代性比较高，生产率高的企业就可以多生产去取代那些生产率低的企业的产品，这些高生产率企业的规模就可以进一步扩大。Pareto的形状参数就决定了企业生产率的差异性，θ越小，企业之间生产率的差异越大，那么高生产率企业就可以凭借自身生产率优势获得更高的价格加成。

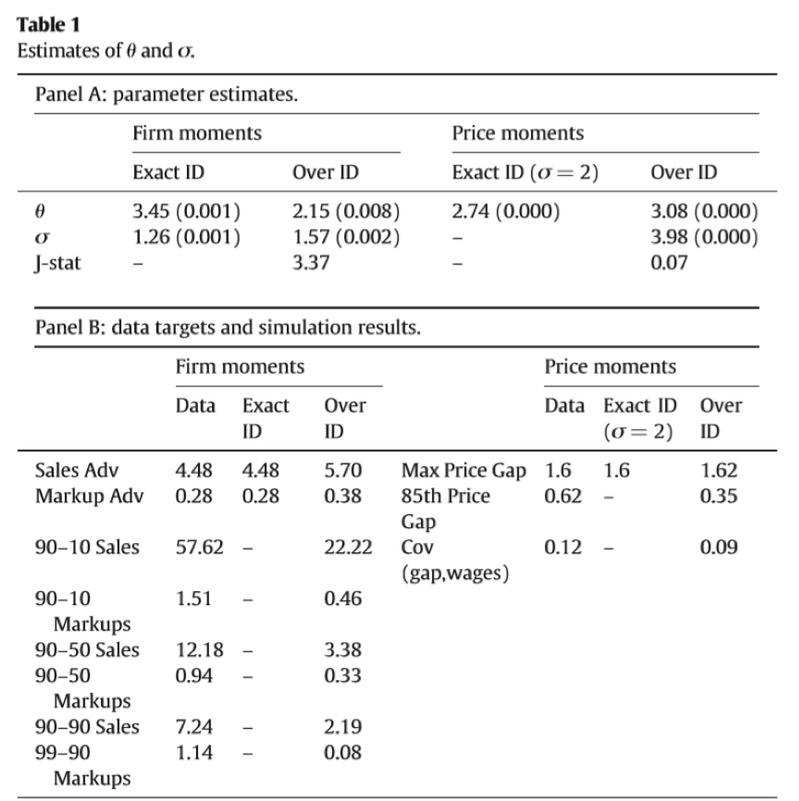
表一分为a和b两部分，a表是参数估计的结果，b表是数据结果与模拟结果的对比。在表中同时包含恰好识别和过度识别两种方法的结果。表a，第一部分是用企业层面的数据去估计θ、σ，得到了3.45和1.26。在使用过度识别让模型去拟合实际分布的尾部，得到另一组参数值，与恰好识别相比θ下降、σ上升，这样的变化更有利于生产率高的企业去发挥自己的优势，获得更高的销售额和价格加成，更符合企业层面的异质性的表现。J统计量为3.36，p值为0.76，不拒绝零假设，即过度识别在95%显著性水平下具有可信度。这进一步说明了GCES效用和Pareto生产率分布的结合的模型在销售额和价格加成方面的异质性更具有解释力度，比其他模型更优越。表a的第二部分，是用微观的商品价格数据去匹配贸易弹性作为稳健性检验。贸易弹性在贸易福利的量化中有重要作用，所以有必要展示我们的结果即使匹配贸易弹性的数据也足够稳健。在这一部分的过度识别结果中，θ=3.08和用企业数据得到的结果基本一致，差别不大。但是σ=3.98与用企业数据的结果有明显差异，因此将σ设为2，使用恰好识别去估计θ得到了2.74，虽然小了很多，但仍然和Simonovska and Waugh(2014) and Simonovska and Waugh (2014b)得到的结果保持一致。

最后，为了测试模型一般适用性，使用已经估计出来的参数来模拟美国的企业，再将模拟结果和美国数据作对比。我们使用的是恰好识别得到的数据，模型的出口商优势是5.4，比BEJK的结果高10%，模型测算的生产力优势是0.19，BEJK是0.15-0.33，基本上吻合，模型的适用性比较强。事实上，美国和智利的数据情况非常相似，我们所发现的大多数数据集的企业的销售额分布都相对一致。

5.3 Model’s fit to the data

在这一部分使用估计出来的参数模拟模型，将模型的一些预测和数据作对比。图2是用过度识别得到的企业的两个分布结果，和图1对比，发现销售额的模拟结果和数据比较相似，拟合效果相对较好，但价格加成的拟合就有所不如，左边的尾部分布难以拟合数据（在图中并没有显示）。总而言之，GCES模型在保持可变价格加成的同时比较成功地拟合了销售额的分布，是用来分析贸易政策的理想的模型，比之其他模型更具有优越性，

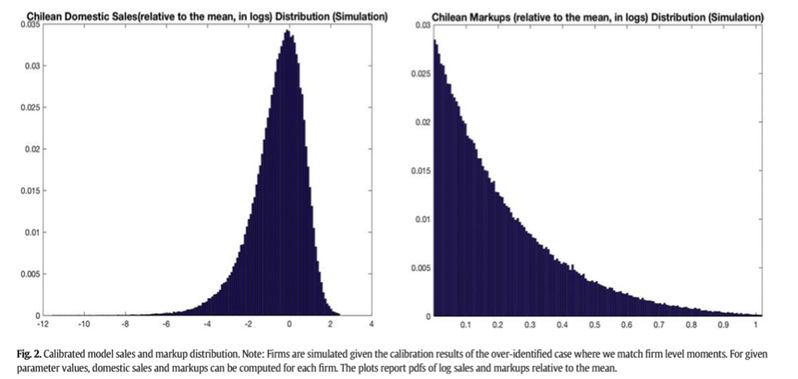
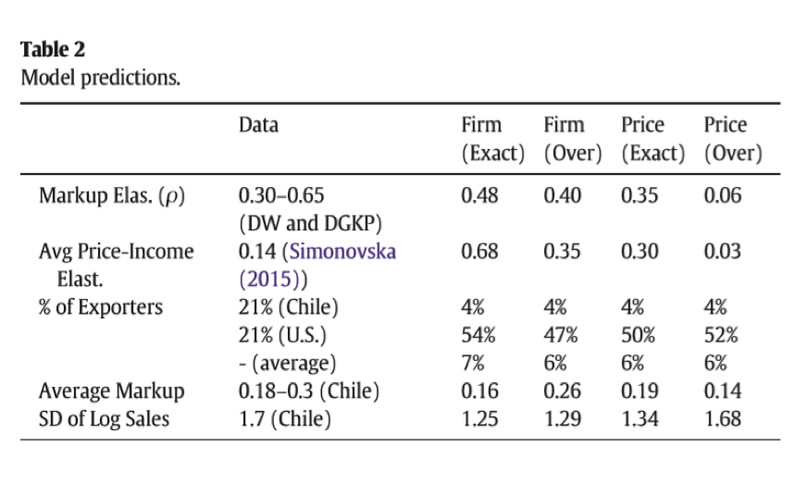
表2是用模型做出的一些预测结果，第一行是收入为权重的价格加成弹性，我们估计的结果是0.4-0.48，ACDR将贸易弹性sita固定在5，得到的是0.36，两篇相关文献，一个是0.3，另一个是0.65（原文献是价格成本弹性0.35，将其进一步估计变成价格加成弹性）。当使用价格矩估计时由于替代弹性的增加，价格加成弹性均比第一种方法的值有所下降，σ=2时ρ=0.35，但当σ=3.98的时候，ρ就骤然下降到0.06，显然替代弹性的设置对于ρ有比较大的影响。

第二行是平均价格收入弹性，由于该值都为正，显然价格确实随着人均收入上升而上升，GCES模型可以解释这种价格歧视。利用价格矩估计的结果证明较高的替代弹性可以降低这种价格歧视，因为较高的替代弹性意味着较小的厂商的市场势力。

最后一行是企业的国内销售额占总的国内销售额的比例，然后取对数，GCES模型的值1.25，比实际的数据1.7要小很多。在这四个结果中，σ最大的估计可以更好的匹配数据，而依赖微观的价格数据意味着较小的价格差异、更高的销售额差异，使替代弹性参数增加的代价是出口商的销售额优势要比现实中的更大。

这些结果意味着要权衡匹配价格和销售额分布的矩，如果一个匹配的效果更好，另一个就难免会下降。σ稍微小一点的时候可以比较好的拟合企业层面出口商相对于非出口商的优势，但如果进一步拟合销售额的肥尾（过度识别）以及价格数据，我们就需要更大的σ才能更好地拟合。也就是说，还是不能同时非常好的拟合这些数据，和Sager and Timoshenko (2017)指出的“需要比Pareto更灵活的一种分布来刻画生产率”使模型能更贴近于数据相一致。

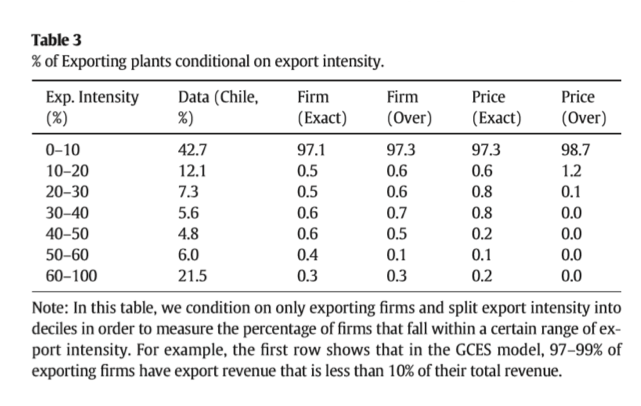
我们也计算了智利出口商的出口密集度（出口的收入占总收入的比例），以进一步判断估计结果对真实数据的拟合效果。表3中，四种估计结果基本保持一致，有97%-99%的企业出口收入占全部收入的比例小于10%，与数据拟合表现最差的部分在最后一行，估计结果显示，几乎没有企业出口收入超过全部收入的60%，但在真实数据中，这一比例高达20%。如果想要更好地拟合这一点，需要我们放松一些假设，比如国家间的对称性参数，并尽力使用模型去解释以出口为主的企业存在。

6.Conclusion

在本文中，建立了一个基本可以统一销售额和价格加成分布的一般均衡模型，这个模型也包含了企业异质性、非位似偏好的特点。GCES可以尽可能统一两个分布，是其他模型所不能比拟的优越性，两个分布的统一有助于我们进一步准确的估计在贸易福利里其关键作用的参数。但是在我们的模型中销售额的平均优势和具体的尾部分布并不能完全统一，对于价格加成的尾部拟合尚且不够，或许，探索更具有灵活性的生产率分布的模型是未来的研究方向之一。

文稿：王一凡

编辑：王妮妮、高雨桐

审校：王永进