云鹰读书会2021第15期（总第70期）

1，摘要与引入

1.1摘要

美国的增长已经下降，而企业集中度和利润却都在上升。劳动收入占国民收入的比例下降，主要是由于低劳动收入占比公司的市场份额上升。

我们为这些趋势提出了一个理论，其中趋势变化的驱动力是跨越多个市场的企业层面成本的下降，这可能是由于IT的加速发展。

效率最高的公司会进军新市场，从而产生暂时的爆发性增长。它们的效率难以模仿，而效率较低的企业很难进入市场，创新也较少。

即使是最高效的公司最终也会减少创新，因为如果他们试图进一步扩张，他们将和效率较低的企业进一步相互竞争。

1.2 文章思路与创作动机

过去几十年美国经济的模式:

1 下降的“长期”增长

2 劳动收入占比低的企业收入占比上升导致劳动收入占比下降

3 在国家层面，行业内企业集中度上升

我们的故事是20世纪90年代的IT(信息技术)浪潮允许高生产率的公司扩大产品生产线。我们将IT浪潮建模为运行产品线间接成本的向下转移。我们假设这在上是凸的，从而对高流程效率的公司的质量创新(创造性破坏)加以遏制。

然而，从长远来看，间接成本的下降可能会导致生产力的提高。减速的同时，它增加了市场总加价，减少了总劳动收入占比。高生产率企业向更多生产线的扩张最终会阻止创新。这导致公司内部较低的成本加成率。高生产率和低生产率的公司最终都会减少创造性破坏，因为他们知道他们将面临更激烈的竞争，而这可能会超过间接成本下降带来的正面直接影响，比如长期创新和生产力增长可能下降，长期增长的下降会导致就业再分配速度的降低。

2，数据

2.1 长期增长的下降

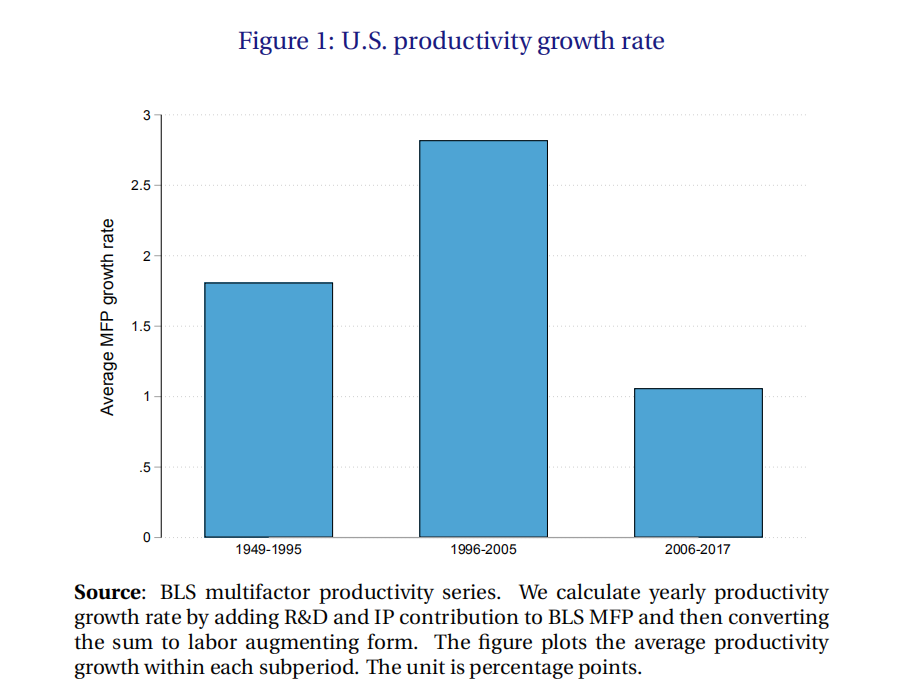
从图中可以看出美国的生产率增速经历了一个先上升后下降的过程。

2.2 劳动力份额的下降

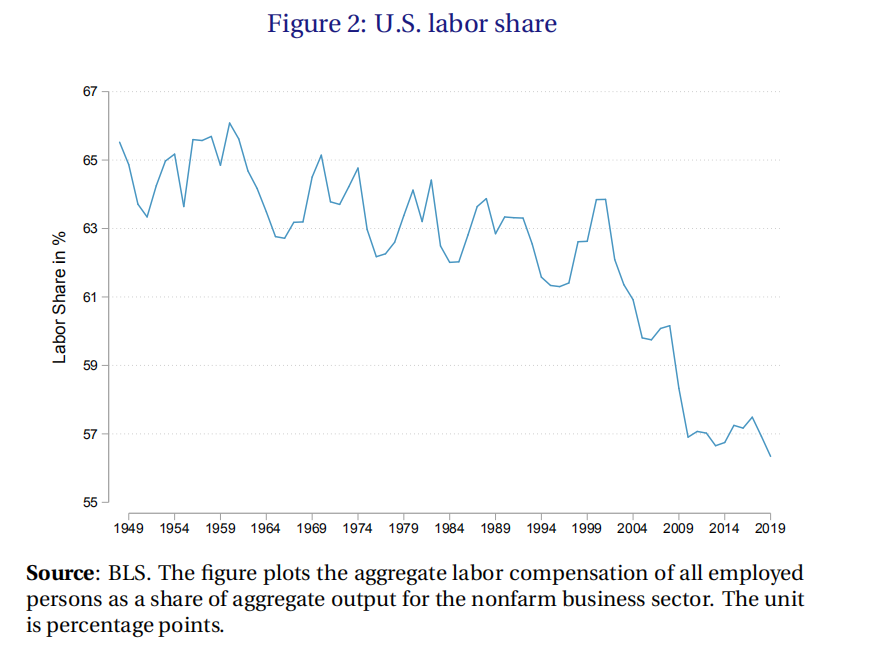
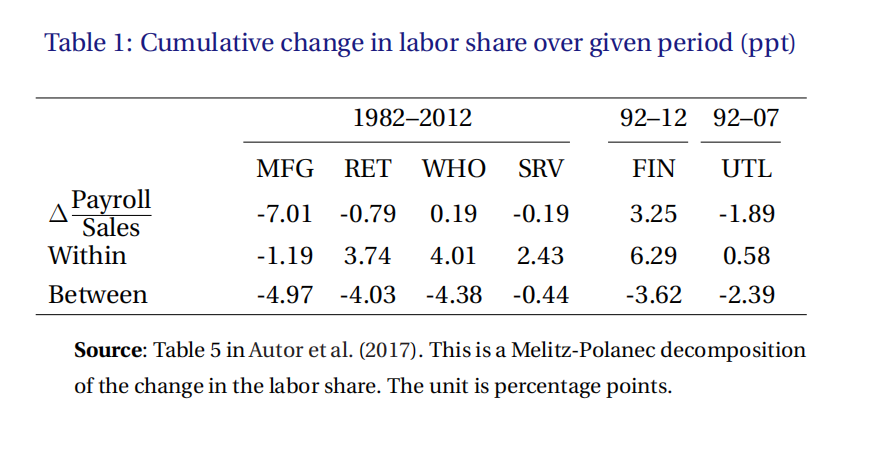
从图2中可以看出美国的劳动力份额呈现波动下降的趋势，而从表1中我们进一步看到各行业劳动力份额的变化以及劳动力份额变化的拆解，我们看到行业内劳动力份额大多数是上升的，而行业间劳动力份额则大多数是下降的。

2.3 企业集中度的上升

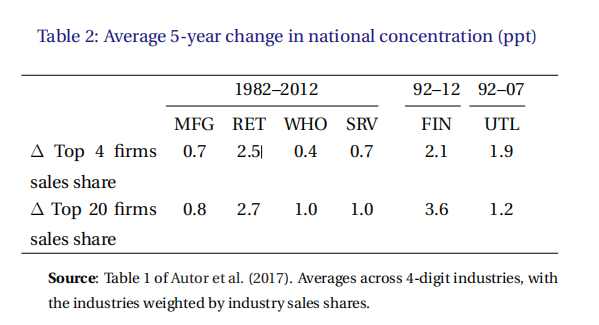
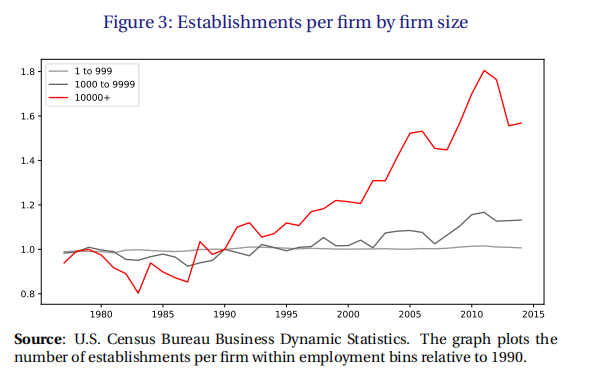
从表2中我们可以看出CR4企业增速较快，站CR20企业增速的多头。从图3我们可以看出，大企业新建厂房的数量远远高于中小企业。

2.4 科技的异动

我们为什么选择科技作为研究的重要变量，有以下四个原因。

首先，图4显示，在1990年下半年IT生产行业出现了爆发性增长之后，21世纪初IT密集型行业出现了爆发性增长。

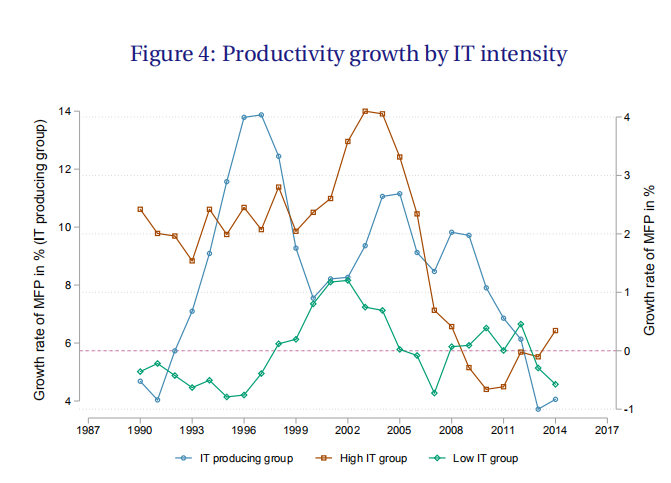
其次，在图5中，我们看到劳动收入占比在所有情况下都在下降，但下降的幅度在IT生产和IT密集型行业尤其大。

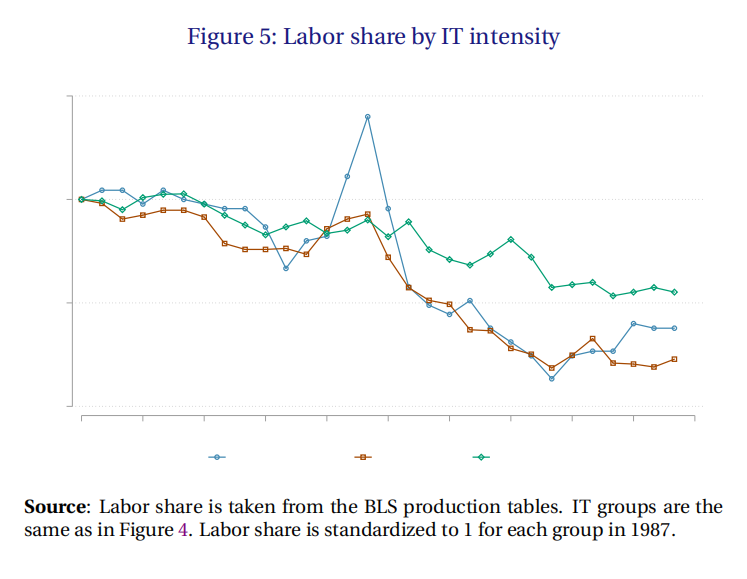
再次，从20世纪90年代中期到21世纪头十年中期的十年间，IT产品的价格急剧下降。参见图6。这是在集中度上升的中期。

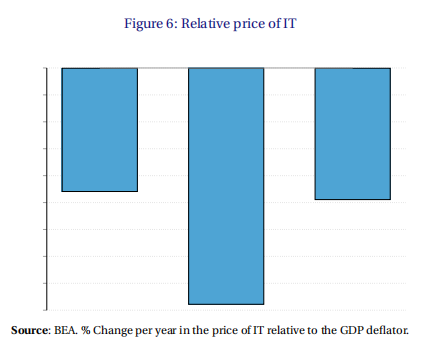
最后，Crouzet and Eberly(2018)和Bauer, Boussard and Laskhari(2018)的研究表明，规模更大的公司在无形资产和IT领域的投资份额更高。IT成本的降低似乎对大公司更有利。

3，模型

3.1 模型总览

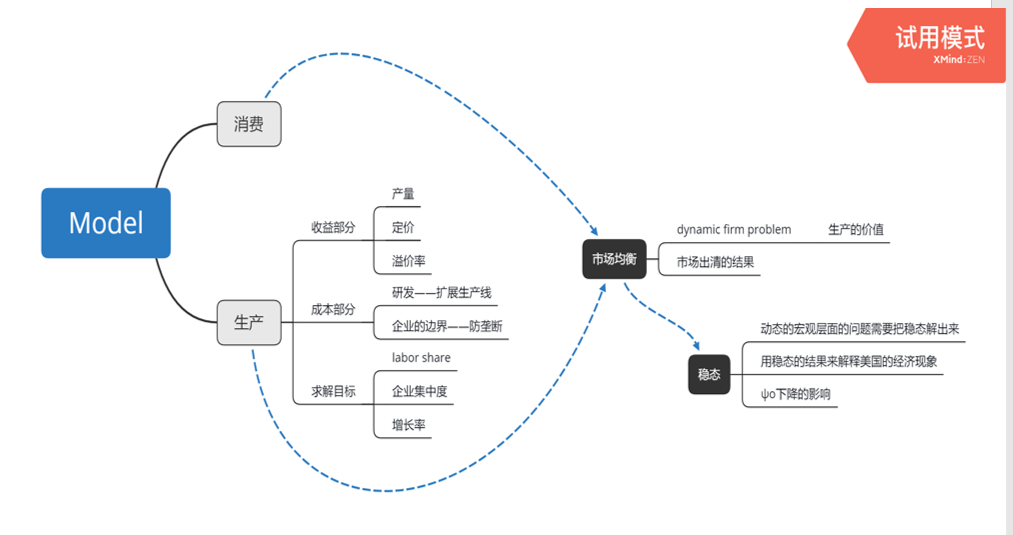
3.2消费效用

时间是离散的，经济由一个有代表性的家庭组成，他们选择消费C来最大化自己的偏好。

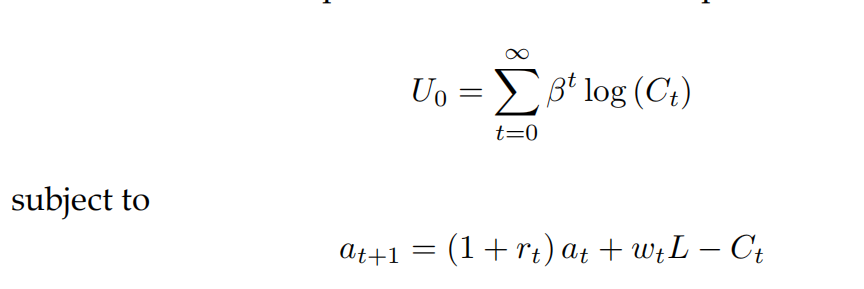
在这里，我们定义符号如下：

：t期财富

：t期利率

：t期工资率

：向劳动力市场无弹性供应的劳动力

随后我们可以得到欧拉公式

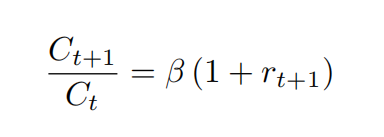
证明如下：

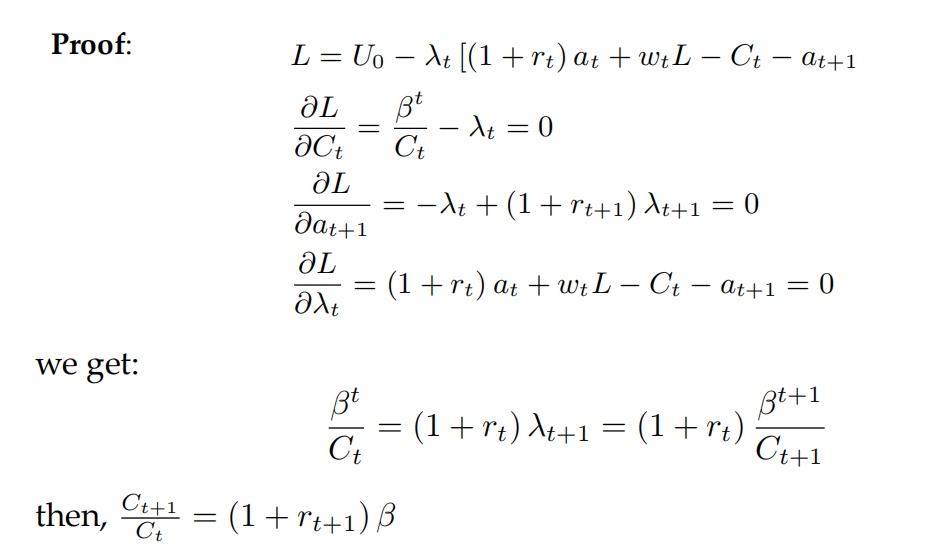
3.3最终产出

这里我们给出三个定义：

最终产出

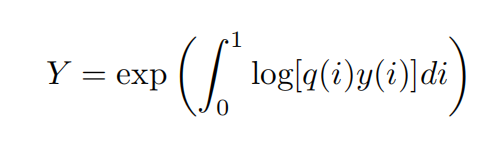
行业的产出

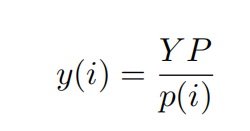
总价格指数

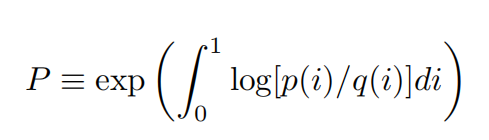
3.4市场结构与中间品投入

此时异质性主要有两个来源。

1 .产品质量，每条产品线都能通过创新和创造性的破坏进行内在提升。

2、经济中的各个公司天生的效率差异

我们用表示企业的生产效率，企业在行业投入的劳动力数量，在表示并且用下式表示该企业在行业的产出：

同时，企业的生产质量有差异，我们用来表示企业在行业生产产品的质量。

这时，我们可以得知企业在行业生产每一单位产品的边际成本是，质量调整后的边际成本是。证明如下：

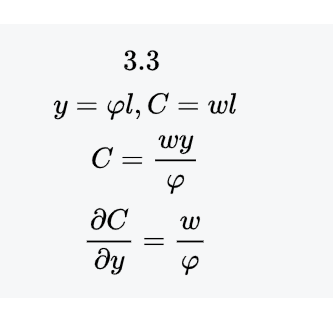
3.5定价

我们这里是市场竞争类型是Bertrand competition，有Leader定价，次优企业跟随Leader，

Leader的定价行为受到次优企业的约束，Leader将其质量调整后的价格设置为与次优企业质量调整后的边际成本相等。我们由此可以得到：

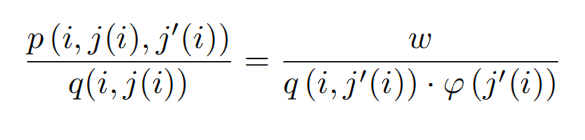
在此基础上，我们定义成本加成率（Markup）如下：

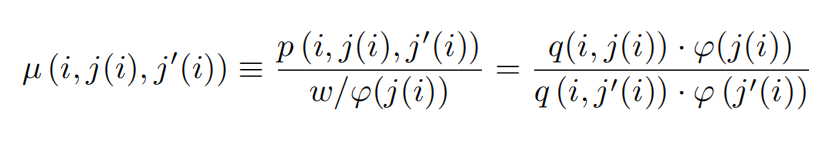
定义成本加成率后，我们用其表示企业的利润：

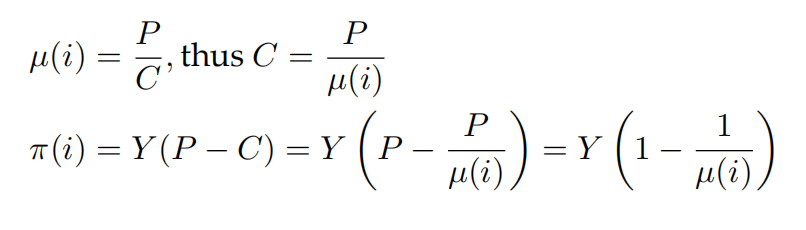
3.6创新和生产效率提升

质量水平的初始分布跨线和企业是外生的。一个企业能够投入成本进行创新，它将在目前自身不是Leader的生产线中随机抽取并提高生产质量，而在每一行业中，质量最高的公司将面临质量较低的公司的竞争，其竞争因子为γ > 1。

此时我们定义创造性破坏：

对任意给定的生产线，它在期进行创新的概率是。

这种因创造性破坏而产生的内在质量改善是该模型长期增长的源泉。

3.7通过二级过程简化生产效率后的成本加成率

我们把生产效率设定成两种类型，市场上存在的高生产效率企业的生产效率为，比例为，低生产效率企业的生产效率为，比例为。那么市场上就会有家高生产效率企业和家低生产效率企业，这时候我们定义两种企业的生产效率之比为。同时我们设定，即产品质量较高的企业永远是Leader。在这种设定下，我们有以下四种情况：

高生产效率Leader与高生产效率的次优企业，此时：

高生产效率Leader与低生产效率的次优企业，此时：

低生产效率Leader与高生产效率的次优企业，此时：

低生产效率Leader与低生产效率的次优企业，此时：

3.8企业的边界

我们假设企业必须支付额外的每一周期间接成本，以下是他们拥有最高质量专利的行业数量的凸函数：

在这里大于0，我们可以知道这是一个凸函数，企业间接费用的边际成本随生产线数量上升。这有利于避免企业垄断所有生产线，符合现实。高生产率的公司通常会比低生产率的公司经营更多的生产线，但没有公司(类型)会经营所有的生产线。

3.9劳动力收入份额

由于最终产出生产中的科布·道格拉斯技术，每个产品的收入都等于。在生产函数中只有一个变量，那么生产线中的总变量成本等于：

对积分，我们得到：

上下两个式子相除，我们得到：

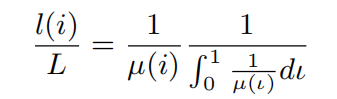
它的经济学含义是行业劳动力占总劳动力的份额。

接下来我们定义总体的劳动力收入份额如下：

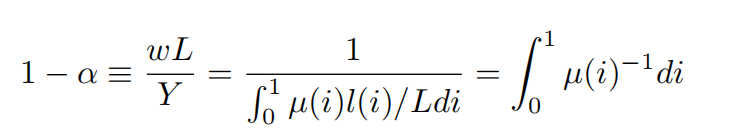
如果企业是高生产效率的企业，那么它的劳动力收入份额如下：

如果企业是低生产效率的企业，那么它的劳动力收入份额如下：

3.10动态公司问题

在动态公司问题中有两个单独的状态变量：

：企业经营的生产线数量

：这些生产线中高效率企业经营的生产线占比

于是我们可以得到：

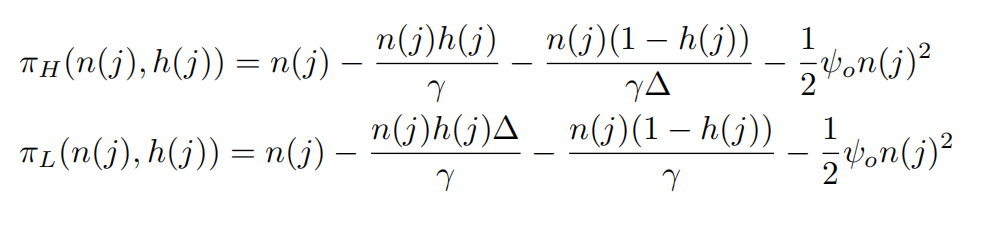
随后我们得知企业价值的计算公式：

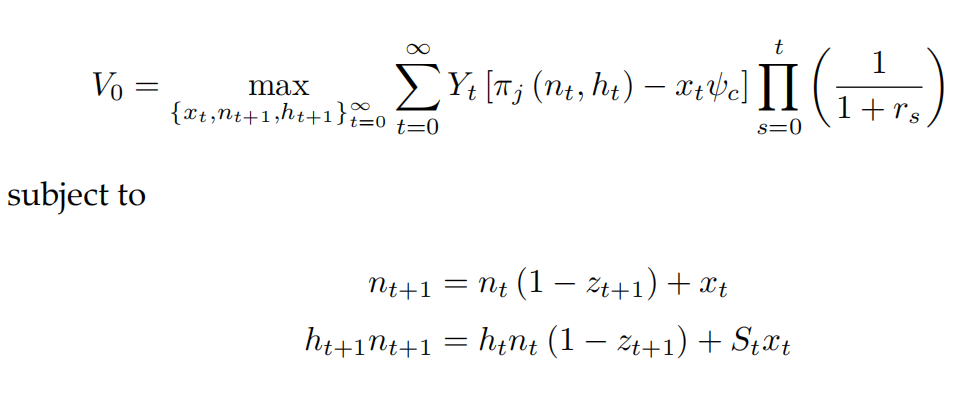
3.11市场出清

最终产出将会用消费、间接成本，研发成本来表示

在这里我们有如下公式：

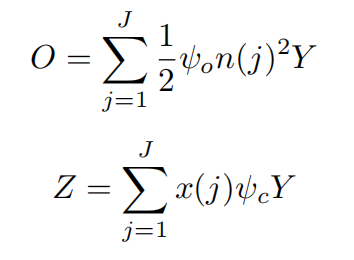
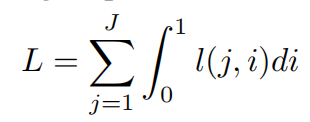
市场出清的条件如下：

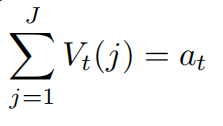
此外，我们也有如下定义，由高生产效率企业经营的生产线数量是：

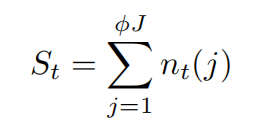
所有的生产线都是由公司经营的，所以我们得到：

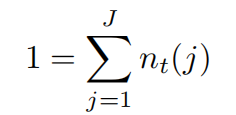
根据以上式子，我们最终解出：

同时我们有：

我们得到总劳动力份额如下：

所以，最终产出可以改写成下式：

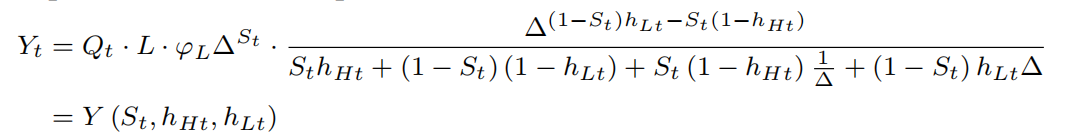
第一个表示“平均质量”的影响;

第二项表示总劳动力;

第三个描述了过程效率的总体水平，它被称为“配置效率”;

最后一个术语则表示了由于成本加成率分散而导致的平均失真。

3.11稳态的定义

在稳态中，利率和增长率保持不变，它们分别为，高生产效率企业经营的生产线数量也是给定的。在稳态中，我们也有以下等式：和。为了使公司内的生产线数量不变，每个公司的研发活动必须与其产品数量成正比，即，同时我们有。

由于成本加成率分布在稳态下是平稳的，因此产出与平均质量成正比。因此，我们已经有：

由此我们可以推出：

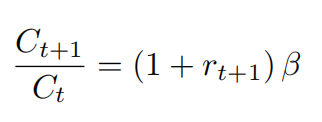
上式结合稳态与我们在消费效用时得到的欧拉方程，我们可以得出：

3.11稳态的特征

我们把定义为一个公司相对于总产出的价值。则我们得到

对于高生产效率的企业来说：

我们将作为该式子的解。

对于低生产效率的企业来说：

我们将作为该式子的解。

根据稳态的定义，我们还能得到：。

最终我们得知。

接下来我们将提出三个结论。

结论1：稳态中，下式将得到满足：

证明如下：对于高生产效率企业，

对求偏导

对求偏导

结合两式即可得到结论，对于低生产效率企业证明方法亦同。

结论2：

(i)稳态中，行业集中度可以表示如下：

(ii)高生产力的公司比低生产力的类型运营更多的生产线，即

(iii)在高生产力作为Leader的行业中，劳动力收入份额可以表示如下：

在高生产力作为Leader的行业中，劳动力收入份额可以表示如下：

证明如下：首先我们证明

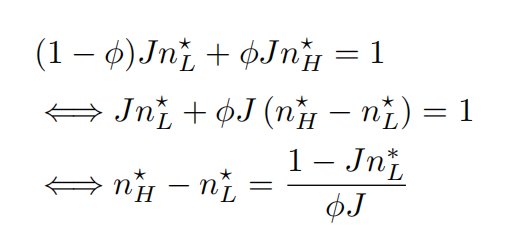
，我们得到：

，因此。

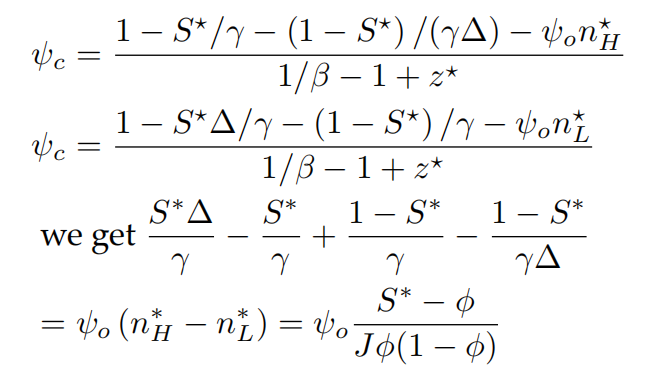
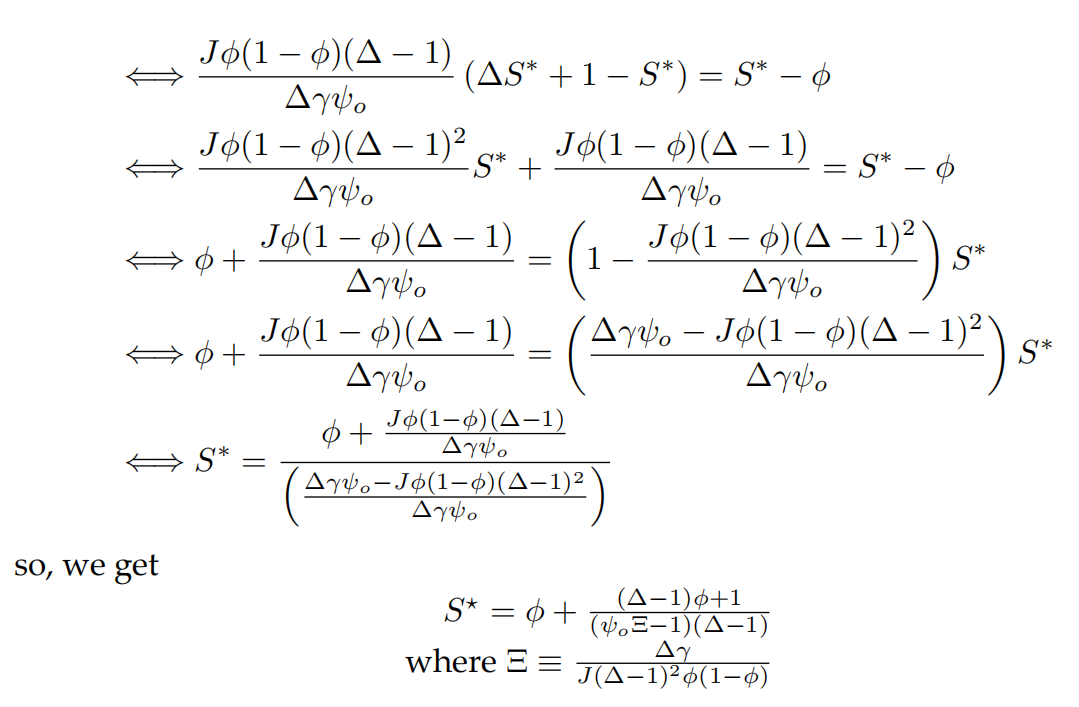
3.12 下降的比较静态分析

在本节中，我们将考虑永久降低间接成本的影响。我们对以下内生性变量的变化特别感兴趣：

1 市场集中度

2 是总体水平和企业内部的劳动力收入份额

3 长期增长率

结论3：永久降低间接成本会导致市场集中度上升。

结论4：随着间接成本的降低：

企业内部劳动收入占比增加，

市场份额的重新分配与此相反，

因此，劳动收入占总收入的比重可能增加或减少。

结论5：对长期增长率有两种方向相反的作用。

的减少对创新的激励有直接的积极影响：随着管理成本的降低，运营一条额外生产线的边际价值就会增加。

然而，也存在着一种方向相反的效应。也就是说，通过增加行业集中度，的减少减少了一家公司进入新产品线的预期成本加成率。这种一般的平衡效应降低了进行研发的动机。这两种效应中哪一种占主导地位取决于精确的参数。

因此，长期增长率呈现先增长后下降的变化，具体将在接下来的内容进行解释。

4.数值分析

4.1校准

我们通过比较唯一差异开销成本参数的稳态，来评估开销成本机制的定量重要性。将初始稳态期定义为1949-1995年，将新的稳态期定义为2006-2017年。我们校准了模型中的6个参数值，以匹配初始周期内的6个统计量。然后，改变，以匹配初始和新稳定期之间劳动份额组成部分之间的变化。通过将模型与集中度、生产力增长、总劳动力份额和无形投资份额的变化数据进行比较，来评估模型的拟合性。

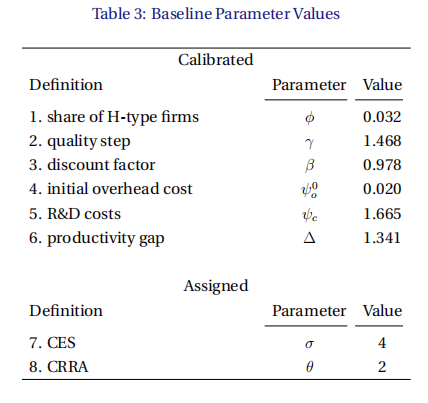
表3显示了校准后的参数值。首先，集中度水平对高生产力公司的份额很敏感。如果接近1，前10%的份额接近10%。较低的，结合足够高的，有助于匹配数据中前10%的集中度，得到了=3.2%。这些高效的公司享有过大的市场份额，因为它们的工艺效率高了约34%（=1.34）。接下来，质量级别对增长目标敏感，较高的增长目标导致较高的估计，将其校准为1.468。对于给定的经济增长率，实际利率随贴现系数的增加而降低，将校准到0.978。，通过高生产率公司生产的产品的份额来影响总加价，将其校准为0.020。最后，包括研发投资在内的无形份额有助于确定衡量研发成本

4.2过渡动态

到目前为止，已经比较了稳态之间的关系。在数据中，我们看到，在21世纪中期之后的生产力放缓之前，生产力增长出现了10年的爆发。很容易表明，随着的下降，理论也将在过渡过程中产生生产力增长的爆发。在过渡过程中增长爆发的原因有两方面：

1. 减少创新动机的一般平衡力——随着的增加而导致更激烈的竞争——只会随着时间的推移而实现。因此，随着的降低，所有公司的研发动机都明显增加，因此质量增长最初就会增加；

(ii)值较高的新稳定状态表现出更高的平均工艺效率，因为有效率的公司操作更大比例的生产线。这种静态效率增益必须在过渡过程中实现，从而在过渡过程中再次实现高增长。

4.2.1改变

为了说明，一个生产力爆发之后的放缓的可能性，我们计算了一个简单的参数化的过渡相互作用。设置了模型参数=0.008、=1.277、=1.014、=0.957、=1.215和初始=0.002，为了匹配统计量，将在下表3中进行讨论。选择管理成本的变化，为了与观察到的增长率的下降完全匹配。

图7显示了第0年管理成本参数下降后，高类型公司()运营的线路份额和创造力破坏率()。急剧上升，并在大约10年后收敛到新的稳定状态。在影响方面，随着所有公司（尤其是高工艺效率的公司）在研发上投入更多，创造性破坏的速度急剧增加。但创造性破坏的上升是短暂的：大约10年后，创造性破坏的速度收敛到新的、较低的稳定状态水平。

与和相比，第二好的生产商和的份额转换要慢得多。这需要超过100年的时间使这个分布收敛到新的稳态。第二优生产商本身会影响加价的分布。因此，劳动力份额的缓慢转变与我们的模型中的成本加成率成负相关

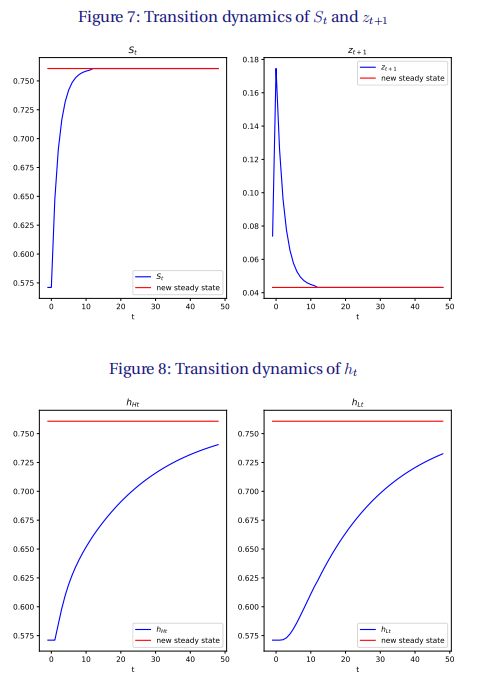
图10绘制了（29）中定义的总水平的分配效率和流程效率。分配效率略有上升，因为随着效率最高的公司占据产品的主导份额，成本加成率分散度会下降。工艺效率因为同样的原因提高4%。分配效率取决于第二优生产者的分布，因此缓慢地收敛到新的稳态。相比之下，工艺效率仅取决于高生产力公司运营的线路的份额，并迅速收敛到新的稳态。

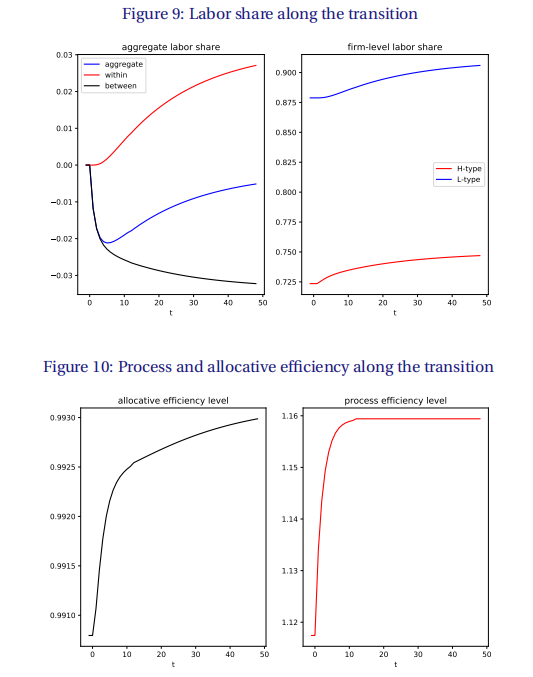
最后，图11比较了减少后的产出和消费路径与初始稳态路径(不变)。随着产量的下降，前五年增长更快，但之后增长更慢。消费在第一阶段公司增加研发和管理投资时急剧下降，然后，由于增长的暂时爆发，消费恢复并高于初始稳定状态路径十多年。最终，创新和增长的放缓造成了损失，消费低于原来的稳定状态轨道

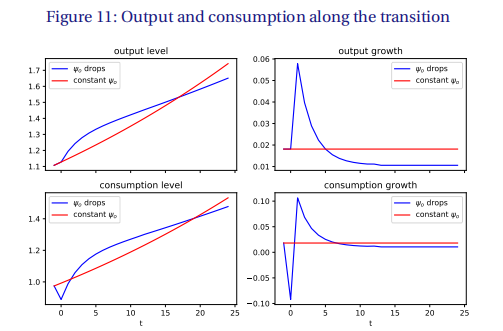
的下降在短期内提高了消费增长，但从长远来看降低了消费增长。因此，我们想知道由于的下降，目前的折扣福利是高还是低。从消费路径中得到的效用是

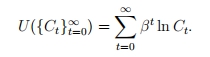
因此，福利的变化可以用（永久的）消费等价的术语，

其中，和是在ψo中有或没有下降的消费路径。我们获得了=-5.1%，因此的下降降低了约5%的福利。这个数字例子表明，尽管分配和过程效率永久提高，创新暂时提高，但长期创新的下降占主导地位，因此整体福利减少

4.2.2 校准结果

表4显示了表3中校准参数下的目标和模型拟合。通过改变，可以准确地拟合生产力增长率和成本加成率。实际利率、无形份额和劳动力份额/销售的相关性非常接近。集中度低了大约10个百分点。尽管如此，该模型还是产生了高度的集中性，超过一半的销售额积累到前10%的公司。尽管它很简单，但该模型能够很好地模拟数据的特征。

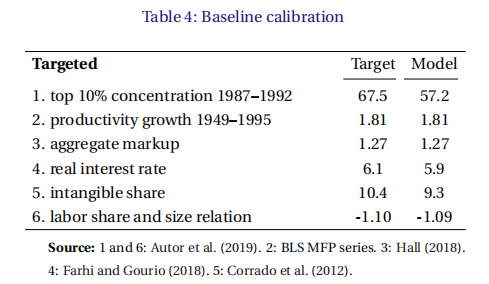
表5显示了降低以与劳动力份额变化的不同组成部分相匹配的新稳态的时刻。相对于最初的劳动力份额水平，中间的组成部分下降了约11%。当下降65%时，该模型与这个下降相匹配。随着的这种变化，该模型充分解释了生产率增长的全部下降程度和总劳动力份额的约三分之二的下降程度。该模型并没有解释劳动力份额下降的全部程度，因为劳动力份额的内部组成部分的增长超过了数据中的增长。在数据中，无形资产的产出份额在模型中上升，尽管略低于数据。模型与数据的显著区别是集中度的上升。在数据中的集中度增加了约5ppt。

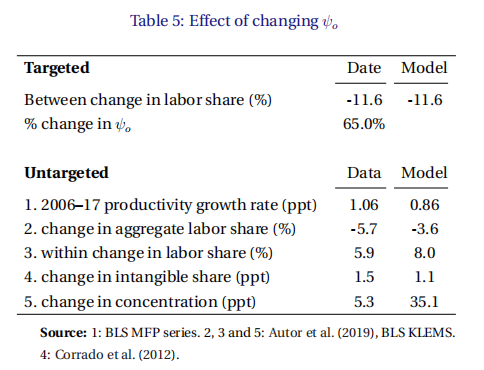
图12显示了随着减少时关键统计量的变化。

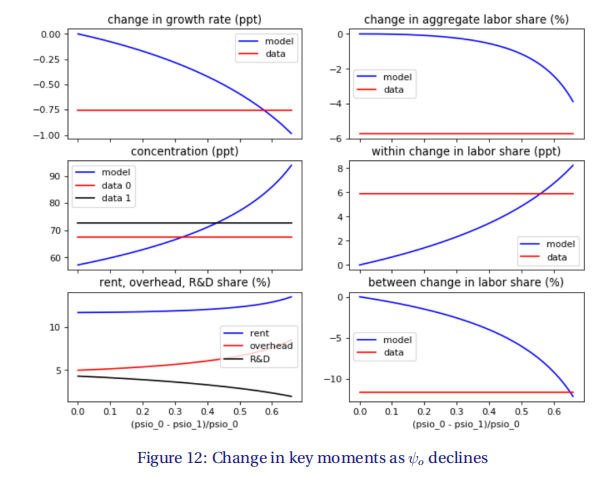
为了阐明模型中的机制，表6显示了选定的内源性变量在初始和新稳态下的值。管理成本的下降鼓励有效率的公司扩张，增加高效公司的产品和销售的份额(更高的和)。尽管开销成本曲线有所下降(由于的下降)，但这种反应仍导致管理成本的上升，作为产出的份额。因此，上升的间接支出伴随着不断上升的无形份额，而研发支出下降。整体无形份额的上升意味着，如果将管理费用和研发费用被视为中间投资，而不是投资，那么总劳动力收入份额的下降将会更小。这与Koh等人的发现相一致。（2016）

随着的上升，低生产率公司的加价明显下降，因为这些公司更有可能生产出第二个最佳生产商是高生产率生产商的产品。在公司内部，高生产力的公司保持不变，因为他们定价不受校准的参数下的限制

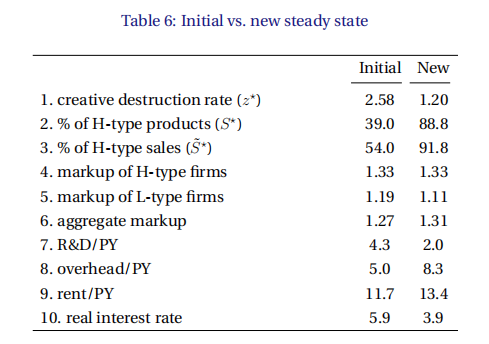
图13显示了成本加成率分布中的变化。它表明，生产重新分配给具有较高加价的高生产力公司。这种重新分配产生了总成本加成率的上升和租金的降低。

在利润上，创新的预期增长幅度也在下降，因为企业更有可能对由高生产率生产者生产的产品进行创新。这种下降阻碍了企业的创新。这些公司减少了研发支出，导致平衡状态下的创造性破坏率较低(较低的)因此，增长也较低。这种较低的增长反过来又转化为在新的稳定状态下的较低的利率。因此，即使在租金和总加价较高，新的稳定状态下增长率也较低。

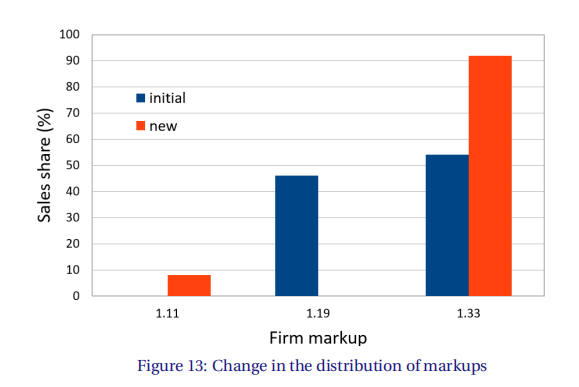
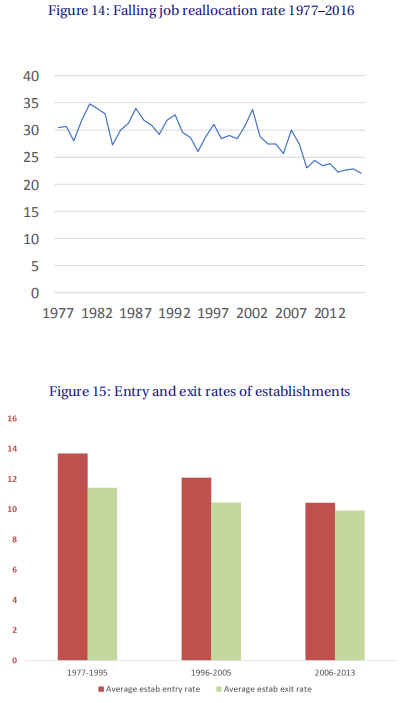
如图14和15所示。跨公司之间的工作当公司的就业水平上升（总创造就业）或下降（总破坏就业）时重新分配。在数据中，这种重新分配部分是由于公司的进入和退出，而我们的基线模型没有这些原因。但数据中工作重新分配的一个重要组成部分是跨幸存的公司。在模型中，由于自己和竞争对手的创造性破坏，公司从其投资组合中加减产品。为了简单起见，我们的公司有一个连续的产品，所以这应该在稳定状态下波动。但对于产品数量有限的公司这是一个短暂的飞跃，因此他们的就业水平上下波动。如果有人强有力地假设每个工厂都与公司生产的给定产品线相关联，那么我们的模型可以更直接地说明跨企业的工作重新分配。然后，数据中的工厂进出可以与我们的模型中的创造性破坏率进行比较。由于模型具有长期增长下降的趋势，这意味着与产品周转相关的长期工作重新分配下降。

4.2.3理论扩展

增加两种效率是为了保持结构尽可能简单。将它推广到，例如具有上界和下界的连续分布。那么一般来说，整个（平稳）分布对于稳态和一个简单的充分统计量如将不再存在

我们也可以允许在工艺效率水平之间存在一些过渡矩阵。在这里假设这个变量是永久性的并不重要。然而重要的是，的差异存在持久性。

另一个推广是放宽的假设。在时，高生产率公司不太可能被创造性破坏所取代，因为即使低生产率类型在质量领域进行了创新，它们仍然是领导者。这样，即使只有两种效率也会导致更分散的加价分布。例如，对于，高生产力类型的公司可以在给定的、或行中有一个加价因素，而低生产力类型的公司可以有一个或的加价。

管理成本函数的二次函数形式产生了这个简单的具有封闭形式解的线性二次动态规划问题。该属性是通过对管理成本添加的额外线性效应来维持的。管理成本函数可以推广到任何凸函数。

其他的一般化也同样简单，例如CES而不是科布-道格拉斯，或者具有CRRA偏好而不是log效用。随着CES的替代弹性，高生产力公司面临低生产力第二优公司可能不再受到限制，而是简单地收取垄断加价.

在这种情况下，随着ψo的减少，高生产率公司的劳动力份额将会减少。

由于所有的公司都经营一个区间的生产线，公司不会同时失去所有的线，因此在稳态时没有公司退出。

然而，我们也分析了该模型的一个变体，其中有“小”公司只经营一条线路。当创造性的破坏发生在他们运营的线路上时，这些公司就会退出。然后，随着创造性破坏的速度随着生产力的下降而降低，企业的进出也会减少。

我们还考虑了模型的另一个版本：公司可以创造新的种类。然后，随着控制范围的增加，就会产生更多的种类。因此，每一个种类的研发支出下降，加强了基线理论的生产力放缓。这里的基线模型是从物理资本中提取出来的。然而，通过假设变量产出的科布-道格拉斯生产函数来包含物理资本是很直接的。该模型将预测，实物资本份额与劳动力收入份额一起下降（利润份额上升）。

最后，我们分析了允许并购的情况。这个扩展模型预测了过渡过程中并购活动的增加。此外，考虑到并购会放大长期生产力放缓，因为减少会导致的更大的增长。

4.3结论

我们提供了一个新的理论框架，该框架可能会占过去30年美国增长经验的很大一部分：

①劳动力收入份额的下降；

②生产力放缓；

③国家层面的集中度上升；

④工作重新分配率下降。

这些现象的很大一部分可以用20世纪90年代中期到21世纪中期的IT改进来解释，这增加了（特别是）最高效的公司的最佳边界。在我们的理论中，这些公司享受更高的加价；当他们扩大到更多的市场时，他们会提高平均加价，降低总劳动力份额。他们通过创新更多的产品线，带来暂时的增长激增。公司内部的加价最终会下降到高生产力和低生产力的公司，因为他们更有可能面临高生产力的竞争对手。这种力量最终降低了创新、增长和工作重新分配。

本文主要对管理成本参数进行了分析。然而，该模型有利于进行更丰富的比较静态分析。特别是，可以直接探索效率差距、创新规模或创新成本的变化的稳态影响。我们的模型的一个优点是，可以很容易地分析这些变化的内部和内部之间的企业影响。

下一步是探索理论的跨行业预测，看看它们是否和数据吻合。

此外，我们还想探究在定量框架内探索税收和补贴政策。

此框架也非常适合讨论竞争政策及其与生产率放缓的关系。

本文分析的这些扩展和其他扩展有待进一步研究。

下期预告

时间：2021年9月27日上午 8：55-11；40

地点：南开大学经济学院圆阶305

论文：Prediction, judgment and complexity: a theory of decision making and artificial intelligence

敬请期待！

文稿：戴冠英、任宴仙

编辑：刘书渊、刘东辰

审校：王永进