云鹰读书会2022第20期(总第101期)
2022-04-272022年4月14日上午,南开大学经济学院云鹰读书会在线上顺利进行,本次读书会由2018级本科生颜茜楠指导推进,由2020级本科生王英至、2019级本科生柳妍婷、2021级硕士生戴萌萌、2018级本科生李阳展示Robert M. Solow的论文:Technical change and the aggregate production function[J]. The review of Economics and Statistics, 1957: 312-320.,由国际经济贸易系王永进老师、杨嗣强老师跟进指导。
特别鸣谢
本次云鹰读书会由南开大学国际经济贸易系
系友苏武康博士赞助支持
引言
索洛主要因为他在五六十年代对资本理论和增长理论的开拓性研究而著名,其中这篇《技术变化与总生产函数》是经济增长理论方面的经典之作。
索洛通过这篇文章更加严肃地讨论总生产函数,想要描述一种新的基本方法,将技术变化导致的人均产出变化与人均可用资本导致的变化区分开来。
本文共分为五个部分,即理论基础、技术进步框架、总生产函数、对饱和状态的进一步解释与全文总结。
第一部分 理论基础
基本假设:
1、中性,规模不变
2、时间连续且完全可微
3、生产函数的紧凑形式满足稻田条件,即资本存量极小时,资本的边际产出极大;资本存量极大时,资本的边际产出极小
4、MPL=w,MPK=r
模型构建:
Q:产出
K和L:单位资本和劳动投入
t:在F中考虑的技术变化
生产函数:Q=F(K,L,t) (1)
A(t)衡量随时间变化的累积效应,在中性情况下,(1)式可变为(1a)式:
Q=A(t)F(K,L) (1a)


第二部分 技术进步框架
1、美国1909-1949年的应用概述
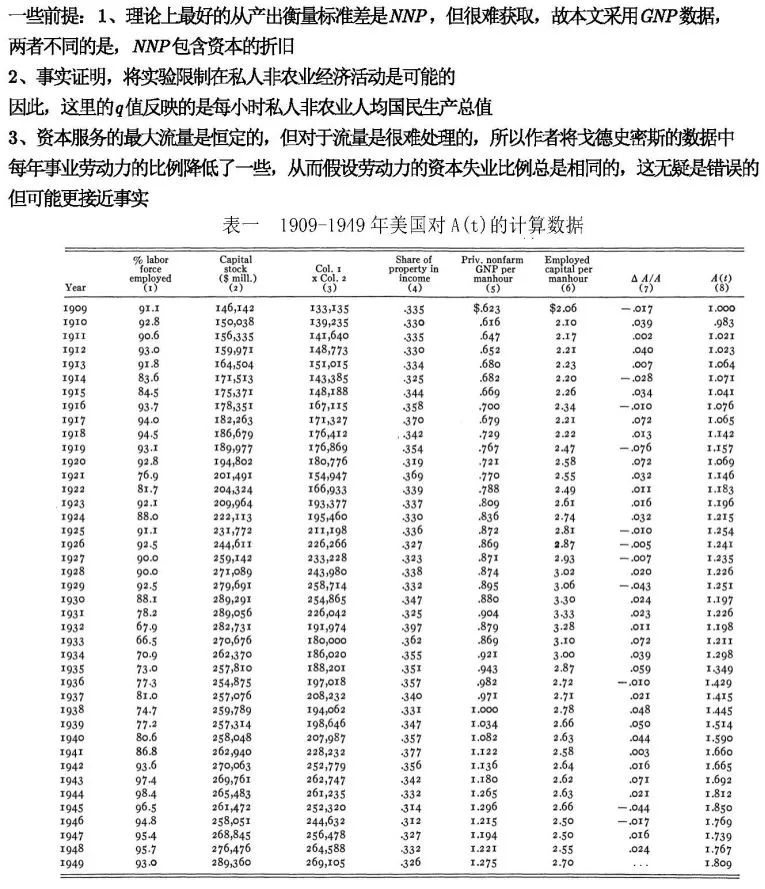

2、1909-1949年美国技术变革情况
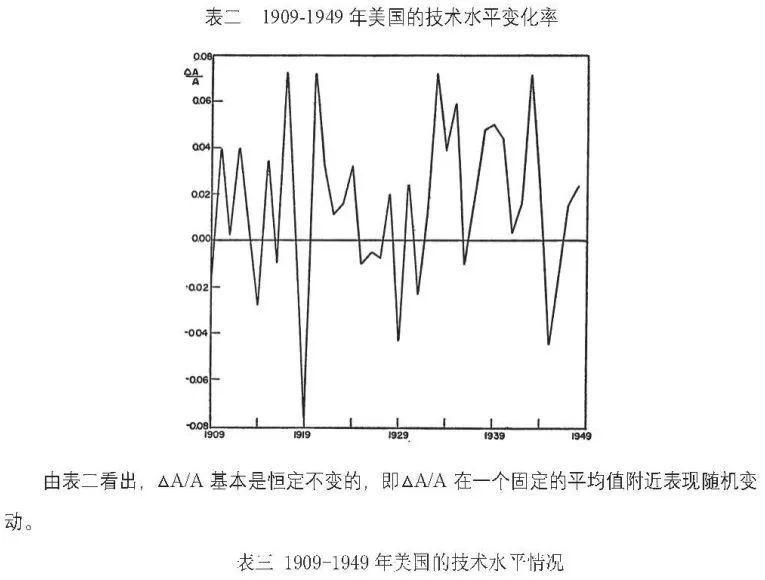
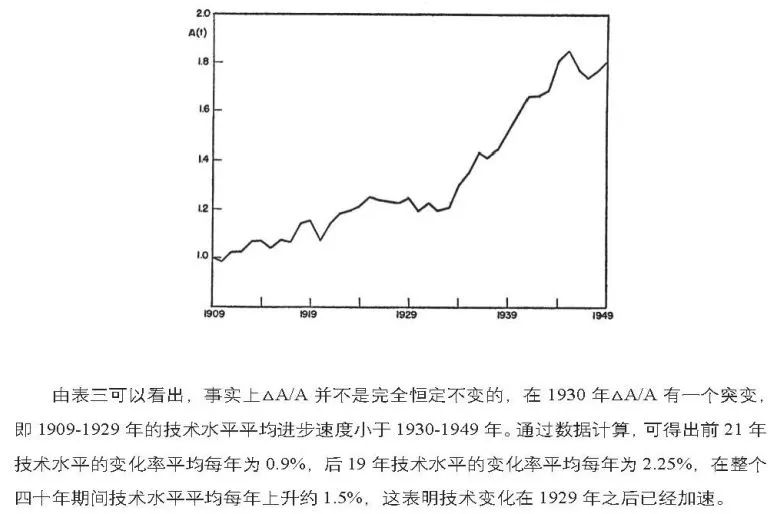
3、由资本增加的GNP增长和由技术水平提高的GNP增长分别占总GNP增长的比例

第三部分 总生产函数
行文至此,作者已经对技术进步的测量及应用做出详细阐述。第三部分则是对总生产函数的一些探讨。
根据规模报酬不变的假设,将(1a)等式两边同时除以L,从而推出(3)式。(3)式中q和k的关系正如上文提到的图1所示。从图1可见,由于技术进步的存在,给定同一个人均资本k所得到的人均产出有所不同,分布在不同的曲线上。这不利于我们研究生产函数f。因此,本文试图剔除技术进步所带来的影响。
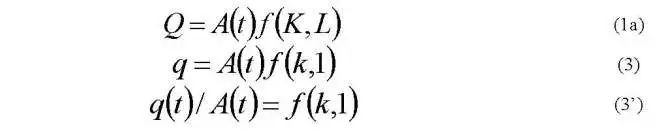
由于我们已经得到了技术进步A(t)的连续估计值,所以剔除影响并不困难,本文的处理方式是对(3)式两边同时除以A(t),得到(3’)式。且本文预期到在剔除技术进步的影响后,q/A与k的观测值所组成的点应该收敛到一条曲线上。如符合预期,我们就可以对生产函数进行研究。
代入本文样本数据后,剔除技术进步后的人均产出q/A和人均资本k的散点关系如图4所示。由于我们先前对原始数据进行了大量的校正,所以对这些散点排列还是非常紧密的。但我们看到有一层明显较高的点,这是超出预期的。研究发现,这些异常点对应于研究期间的最后七年,即1943-1949年。接下来,本文对异常点产生的原因做了可能的猜测:首先可以看出,这些异常点组成的点层与正常点层近乎平行,可以猜测是生产函数移动导致的吗?答案是否定的,因为在对图4的处理中我们已经剔除了生产函数移动即技术进步带来的影响,所以这种解释是行不通的。另一种可能的解释把异常层的存在归因于1943-1949这七年的资本使用与前面年份是系统不可比的。
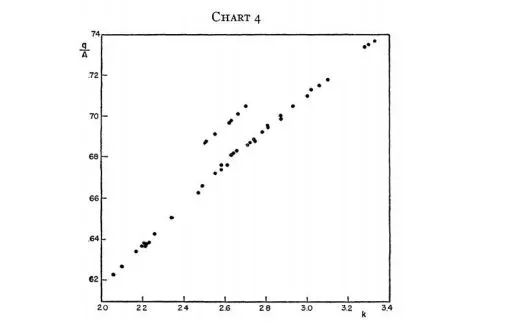
详细来看,这七年包含了战中和战后两个期间。首先,1943年到1945年这段时间属于二战期间,战争期间通过对资本的多轮使用,使得资本服务的使用更加密集,但由于资本服务这一数据难以获得,所以本文使用实物资本存量指标来衡量k,这种衡量方法的缺陷在于无法反应对资本服务的密集使用,因而资本投入被低估,这种对资本投入的低估导致了对生产率增长的高估,所以1943-1945年,这些点落在较高的异常层上。实际上,如果资本度量准确,他们应该落在图中更靠右、靠上的位置。对于1946-1949战后期间,我们可以用战争以后仍然对资本进行多轮使用作为解释依据,但作者认为这不太可能解释偏离产生的全部原因,因而提出了另一种猜测,即1945年以后采用的加速折旧法可能导致对资本存量的低估,进而导致异常点的产生。以上是本文对于异常层产生原因的全部解释。
在开始讨论生产函数之前,我们需要注意本文提出的一个注意事项。作者是不同意对样本数据随意截断的,因此在文章第一版时保留了异常值进行分析。但经过试验发现保留异常值只会引起结果的失真和扭曲。因此,尽管这种做法有些不妥,作者最终还是删除了1943-1949年这七年的观测值进行分析。
进入对生产函数具体形式的讨论。首先,从图4可以看出该曲线呈现出一种持续的但并不剧烈的边际收益递减现象,即单位人均资本的增加所带来的人均产出的增加在减少。这里我们暂时不考虑当人均资本达到饱和时的情况,论文最后会对资本饱和状态进行单独分析。本文选取拟合函数形式的考虑因素有以下几点:(1) 两参数曲线簇;(2)为了计算方便,选择参数是线性的拟合曲线;(3)除了用以对比的直线外,选取至少能够呈现出边际收益递减特性的拟合线。
本文共选取了下面五种函数进行拟合。(4a)是线性形式,(4b)是半对数形式,(4c)是双曲线,(4d)是柯布道格拉斯形式;(4e)是一个边际收益先递增又递减的函数,经过简单计算可得拐点是k=β/2,并且我们的样本数据中k的观测值均分布在拐点右侧,即边际收益递减的阶段,因此符合拟合函数选取的要求。其中,(4b)和(4c)均与横轴正半轴有交点,从经济学角度解释,必须要达到某个正的人均资本以后,人均产出才能为正数,检验后发现样本期间内所有的人均资本观测值均在交点右侧;此外,(4c)和(4e)两种函数形式均存在上界。
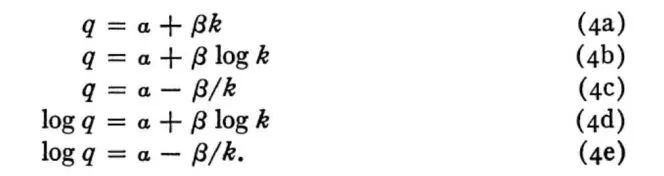
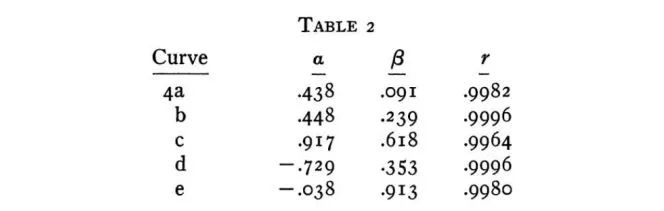
用上述五种曲线形式对散点进行拟合所得结果如表2所示。可以看出这五种函数形式拟合后得到的相关系数都非常高,看似都能比较好的对图4进行拟合。仅从相关系数的角度,(4b)半对数形式和(4d)柯布道格拉斯形式表现较好,相关系数最高,为0.9996。
下图是对表2的拟合结果所画的简图,通过该图可对五种拟合函数形式有一个直观的理解。
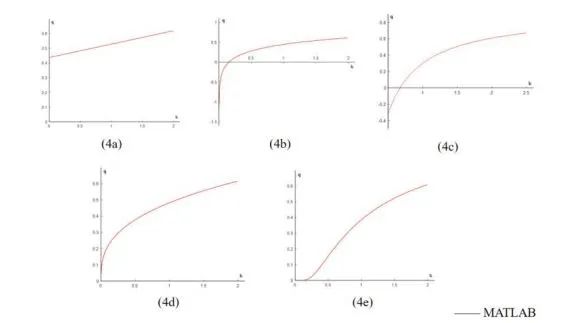
上述五种拟合曲线均可视为g(y)=α+βh(x)形式的,可以作为线性回归来理解。为了进一步对五种拟合形式进行选择,本文采用了Prais and Houthakker合著的一本书《The analysis of family budgets》中提到的从对非线性性测量的角度对拟合优劣进行检验的一种方法。这种方法可以理解为,我们希望按照自变量取值递增的方式排列的残差序列是随机的。但如果残差序列展现出强烈的序列相关,或者当残差长期为正和残差长期为负交替出现时,就可以认为偏离了线性的情况,拟合形式表现并不太好。本文也用“残差序列相关的程度”作为非线性性的一种衡量,并基于此判断拟合形式的优劣。
本文对(4a)线性拟合,(4b)半对数形式,(4d)柯布道格拉斯三种形式进行了上述检验。我们发现(4a)线性形式是一个较差的拟合,(4b)和(4d)都通过了检验,在二者之间几乎没有选择的余地。因此,本文比较有力地验证了前文视觉感受到的图4边际收益递减的真实性。
第四部分 对饱和状态的进一步解释
资本饱和状态:
总生产函数没有显示出资本饱和的状态,也不存在真正的渐近线。于是文章将0.95作为q的饱和状态 并使用4a:q=α+βk 作为最低限度的资本饱和状态,其饱和值大概为5.7,是目前资本值的两倍。
文章进一步联系到总产出 我们更关心资本的净生产率,但这两者之间区别的关键是:贬值(depreciation),但缺乏关于贬值在长期的估计 故不能做出关于净产出的整体分析。但仍可以分析:边际生产总值降低至“边际折旧率”时,资本的边际生产率为0。例如:当增加一些资本时,增加的产品仅足以弥补资本增量本身的折旧。近年来 国民生产净值(NNP)增长速度约为国民生产总值的90% 故资本折旧约为国民生产总值的10%。由Table1 可知 资本每年的产出约为2%-3%,也就是说,资本每年的折旧率也在2%-3%,即资本饱和状态在资本边际产出降至3%-5%,此时,劳动资本比率约为5(甚至更高)。
第五部分 结论
本文提出了一种简单的方法将聚合生产函数的变化与沿着它的运动分开,此研究依赖于要素都支付给边际产品了,但也可以推广至垄断要素市场
本文使用了美国1909-1949的数据,得到以下结论:
1.技术变化在这期间基本是中性的;
2.生产函数向上倾斜,除了少数波动外,生产函数的上升变化速度在前半期每年约为1%,在后半期每年约为2%;
3.人均总产出的增长87.5%归功于技术进步,12.5%归功于资本投入;
4.根据技术变化校正的总生产函数,给人一种明显的收益递减的印象,但曲率并不剧烈。
参考文献
[1] Romer P M. The origins of endogenous growth[J]. Journal of Economic perspectives, 1994, 8(1): 3-22.
[2] Solow R M. Technical progress, capital formation, and economic growth[J]. The American Economic Review, 1962, 52(2): 76-86.
[3] Sato R, Beckmann M J. Neutral inventions and production functions[J]. The Review of Economic Studies, 1968, 35(1): 57-66.
[4] Temple J. A positive effect of human capital on growth[J]. Economics Letters, 1999, 65(1): 131-134.
[5] Hicks J R. Marginal productivity and the principle of variation[J]. Economica, 1932 (35): 79-88.
下期预告
时间:2022年4月21日上午8:55-11:40
地点:腾讯会议
论文:
(a)Harberger, A. C. (1964). The measurement of waste. The American Economic Review 54(3), 58–76.
(b)Hulten, C. R. (1978). Growth accounting with intermediate inputs. The Review of Economic Studies, 511–518.
敬请期待!
文稿:王英至 柳妍婷 戴萌萌 李阳
编辑:刘书渊 刘东辰
审校:王永进
2022年4月27日
