云鹰读书会2024第11期(总第195期)
2024-05-082024年4月7日下午,南开大学经济学院云鹰读书会在圆阶205教室“数字经济与贸易科研训练:理论”课堂上顺利进行,本次读书会由2022级本科生杨惠晴、杨璐菱、曾艺孜同学展示Rasmus Lentz和Dale T. Mortensen的发表在Econometrica的论文“An Empirical Model of Growth Through Product Innovation”,2008,由国际经济贸易系何秋谷老师跟进指导,助教薛靖羲提供答疑。
特别鸣谢
本次云鹰读书会由南开大学国际经济贸易系
系友苏武康博士赞助支持
摘 要
公司之间生产力的差异是巨大且持久的,但劳动力再分配作为总生产率增长的一个重要来源的证据是不明确的。本文目的是估计一个通过创新实现增长的一般均衡模型,旨在识别和量化资源再分配在增长过程中的作用。本模型拓展了Klette和Kortum(2004)建立的企业进化和增长的熊彼特理论,并扩展到允许企业的异质性。数据集是关于丹麦公司的面板数据,包括增加值、员工和工资的信息。模型拟合的很好。估计的模型表明,在每个行业中,生产力较高的公司增长得更快,从而在稳定状态下将生产力较低的公司挤出市场。这种选择效应占总增长的53%。
目录
一、引言
二、丹麦公司的数据
三、创造性破坏的均衡模型
四、估计
五、工人再分配和增长
六、总结与评价
01|引言
Bartelsman和Doms(2000)在他们基于长期的工厂和企业数据得出结论:生产单位、企业或企业之间的生产力分散程度很大。此外,任何公司的生产率分布都是高度持久的。尽管对生产力的企业异质性的解释尚未完全理解,但根据经济规律,它的存在将导致资源从利润较低的公司重新分配到利润更高的公司。
在本文中,作者量化了工人重新分配对生产率增长的影响,是早期论文Le-ntz和Mortensen(2005)的更丰富版本,同时建立了一般平衡解的存在性。该模型是Klette和Kortum(2004)的拓展,该模型本身建立在Grossman和Helpman(1991)、Aghion和Howitt(1992)的内生性增长模型之上。它的目的是捕捉由创造性破坏过程引起的重新分配对增长的影响。
在该模型中,最终的消费产出是由一个竞争部门使用差异化的连续的中间产品作为输入而产生的。作为在位公司和新进入者的研发(R&D)投资的结果,更高生产力或更高质量的各种中间产品类型会产生。当前版本的供应商具有基于前沿知识的垄断权力,并将价格设定在高于边际生产成本之上。随着新产品取代旧产品,创造性破坏的过程导致需要在不同活动中重新分配工人。企业在其所创造的中间产品和服务的预期生产力方面存在差异。本文模型有两个主要的经验含义。首先,一家更具创新性的公司,其产品所体现的质量提升更大,可以收取更高的价格,更有利可图,因此在创新上的投资更多,平均进入后增长相对较快。其次,公司增长率的类型条件期望与公司规模无关。
利用该模型的一般均衡,作者根据1992-1997年期间丹麦公司面板数据提供的增加值、员工数量和工资信息,通过间接推断方法估计参数。该模型是根据一些横截面和动态矩进行估计的,包括规模、生产力和企业增长分布的矩。这些数据不包含任何对公司创新活动的直接观察。在该模型中,创新活动决定了控制企业规模和生产力动态的随机过程。这些面板数据的矩和模型的结构允许对创新进行推断。利用专利数据,Balasubramanian和Sivadasan(2008)通过调查专利活动对企业规模和测量的生产力的直接影响,提供了支持Klette和Kortum(2004)创新和企业动态模型的证据。尽管专利数据是对企业增长的投资的狭隘反映,但专利活动可以被视为一种代理。
在作者的模型中,最终商品消费的总增长率等于中间投入的生产力增长率,按消费比例的加权平均。这一项可以按公司类型分解为进入者和在位者的净贡献。进入的净贡献是在每个时期内相对于退出市场的进入的生产率的平均增长。在位者的净贡献可以分解成两部分,旨在解释选择过程的结果与企业增长率和成活率的差异:第一,公司份额不变,仅有生产力变动带来的贡献;第二,选择效应,是稳态时公司份额和进入时份额之间的差异的贡献。因为一个更高产的公司类型增长得更快,它在稳定状态下的份额超过了进入时的份额,这意味着选择不同增速导致的选择效应对总生长速率有正贡献。事实上,我们估计的模型表明,净进入市场公司占总增长率的21%,其中53%可以归因于选择效应。
尽管模型中所有的生产力增长都与重新分配有关,但文章强调选择效应是增长的重要贡献,其来自于生产率更高的公司以牺牲生产力较低的公司为代价进行重新分配,从而增加其经济份额的程度。在该模型中,企业类型的不同在于产品质量改进分布有所不同。选择效应是通过生产力水平不同的企业类型的不同创新率来实现的(随机占优顺序)。如果所有的公司都面临着相同的产品质量改进分布,则它们会选择相同的创新率,那么选择效应为零。创新活动具有积极的溢出效应,所有公司都在同一质量前沿上创新,创新推动前沿向前发展。因此,虽然在我们的模型中,生产效率更高的公司平均产生了更大的质量改进,但所有公司都在同一边界上进行创新的事实意味着,在稳定状态下的高生产率和低生产率公司之间的平均生产率差异是恒定的。选择效应影响稳态增长率而非生产力水平,因为生产力更高的公司对质量增长的贡献更大。
02|丹麦公司数据
丹麦公司的数据提供了关于生产力分布以及生产力、就业和销售额之间的关系。现有的数据集是一个来自丹麦商业统计登记册的1992-1997年由私营企业组成的年度数据。样本仅限于那些拥有20名或以上员工的公司,共约4900家。该样品不包括新进入市场的公司。每年观察到的变量包括增加值(Y)、总工资账单(W)、全职就业人数(N)。文章利用这些关系来训练所研究的理论模型。Y和W都是使用真实丹麦克朗(DKK)来测量,而按人头计数。
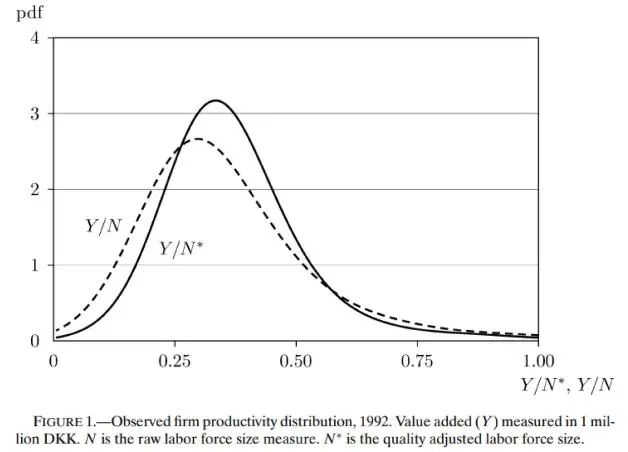

是市场上每个工人支付的平均工资。虽然以这种方式纠正公司间的工资差异确实在一定程度上减少了隐含生产力分布的扩散和倾斜,但这两种分布都有很高的方差和倾斜,并且本质上是相同的形状这两种分布都与在其他数据集中发现的分布一致。例如,生产率分布明显分散,并向右倾斜。调整后的生产力的第5百分位大约是第一种度量的一半,而第95百分位大约是第一种度量的两倍。两者之间的范围代表了四倍的每个员工在不同公司增加值的差异。这些事实与Bartelsman和Doms(2000)用美国公司进行测算的结果相似。
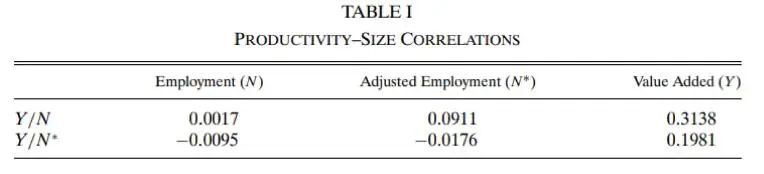
对于跨公司的生产力差异,有许多潜在的解释。对表I所表示的两种分布进行比较,似乎说明劳动投入质量的差异并不重要。如果技术改进要么是中性因素,要么是资本增加,那么生产力更高的公司将获得更多的劳动力和资本。其隐含的结果似乎是劳动力规模和劳动生产率之间的正相关关系。有趣的是,在丹麦的数据中,两者之间没有关系。
表I报告了两种劳动生产率指标与在增加值中反映的两种就业指标和销售之间的相关性。如表中所示,无论是使用原始的或调整后的就业衡量标准,劳动力规模和生产率之间的相关性都为零。然而,请注意,增加值和劳动生产率的两种指标之间存在很强的正相关关系。
本文中发展起来的理论部分是由这些观察结果引起的。具体来说,它是一种假定特定形式的劳动力使得技术进步的理论。因此,生产效率更强的企业在每单位增加值相同劳动力投入下生产更多,这一明显的事实与该模型是一致的。
03|创造性破坏的均衡模型
众所周知,公司呈现出多样化的形态和规模。在任何对企业规模和生产力之间关系的分析中,这一事实都不容忽视。此外,一个充分的理论必须考虑到公司的进入、退出和发展从而解释所观察到的规模分布。Klette和Kortum(2004)构建了一个企业产品创新和增长的随机模型,该模型与企业规模演变和分布的格式化事实相一致。该模型还具有性质:技术进步能节约劳动力。基于这些原因,作者在本文中继续采用他们的方法。
尽管Klette和Kortum(2004)考虑到了生产性的异质性,但企业生产力和增长是不相关的,因为在他们的模型中,增长的成本和收益都与企业生产力成比例。因此,允许企业增长和生产力之间的正相关关系是必要的,以图与本文从丹麦公司数据中发现的关系相一致。
3.1 偏好和技术
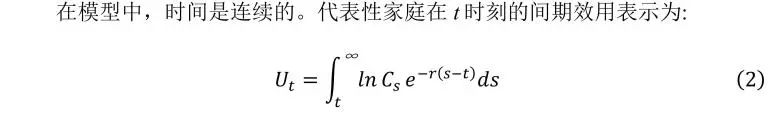


3.2 中间产品价格
每一家公司都是它过去创造的产品幸存到现在的垄断供应商。对每种产品收取的价格是垄断价格和由于与以前版本的产品的供应商竞争而产生的限制价格的较小值。在Nash-Bertrand均衡中,限制价格正好是将其他所有供应商驱离市场的价格。也就是说,在所选择的价格上,消费者对质量领导者以极限价格提供的高质量中间产品和以边际成本定价的次高质量替代品是漠不关心的,前提是这个价格小于利润最大化价格。极限价格是最新质量改进的幅度和边际生产成本的产物。如果垄断价格低于限制价格,公司只需收取垄断价格。

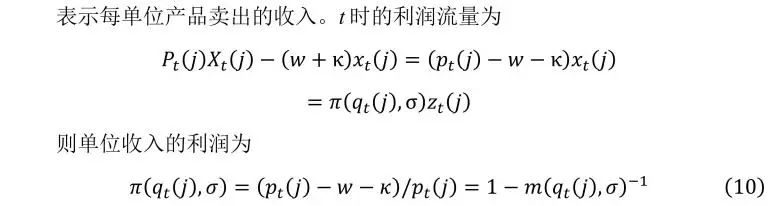
3.3 总增长率


3.4 公司价值



3.5 公司进入

3.6 公司规模的稳态分布

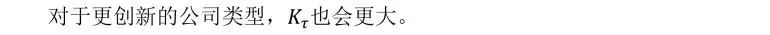
3.7 劳动力市场出清

3.8 总增长率构成
创造性破坏率是企业类型的进入率和创新频率的总和:

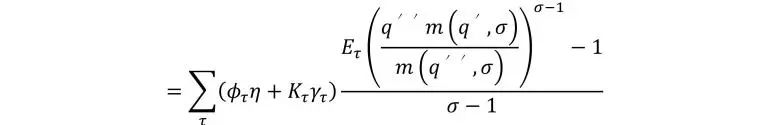
换句话说,总增长率等于创新到达率和创新对总消费的净贡献的乘积。由于这两个构成部分对于生产力更高的公司类型都更大,则生产力更高的公司对总增长率的贡献更大。
3.9 均衡

04|估计
如果创造更高质量产品的能力是一种永久性的企业特征,那么企业盈利能力的差异就与企业所选择的产品创造率的差异有关。具体来说,盈利能力更强的公司增长速度更快,未来更有可能存活下来,而且平均会供应更多的产品。因此,当前每产品总利润和销售量之间应该存在多公司的正相关。此外,工人从增长缓慢的公司重新分配到利润更高的增长迅速的公司将是总生产率增长的一个重要来源,因为增长更快的公司对增长的贡献也更大。
在这一节中,作者将证明,可以通过公司盈利能力的特定差异来解释丹麦公司的增加值、就业和支付的工资之间的关系。在对模型进行数据拟合的过程中,文章还得到了所有企业面临的创新函数的投资成本估计以及企业进入时生产率的抽样分布。
4.1 丹麦公司的数据

然而,由于单位产品的生产雇佣人数随生产率上升而减少,当增长独立于公司过去实现的产品生产率提高时,总预期的劳动力(雇佣)需要不随π增加而增加,而是随z增加而减少。这个理论的含意可以直接加以检验。
该模型是在一个由4872家公司组成的非平衡面板上估计的,该面板选自前文描述的丹麦公司面板数据。该小组是通过选择1992年的所有现有公司并一直跟踪它们而建立的,而随后几年所有公司被排除在进入抽样之外。在估计中,观察到的1992年横截面数据将被解释为反映稳定状态,而随后的几年通常不反映稳定状态,因为存活可能性因公司类型而异。
具体而言,由于选择效应,相对于稳定状态,1993年至1997年观察到的横截面数据中,高创造率公司类型的比例将越来越高。观察1992年横截面逐渐退出的能力将是一个有用的识别来源。原始数据集中的输入存在选择偏差,虽然我们可以尝试纠正该偏差,但我们已经选择了完全不排除输入,因为它不需要进行识别。通过在力矩集中包括1997年的横截面,随着时间的推移而改变幸存者的横截面组成的动态过程被反映在估计中。
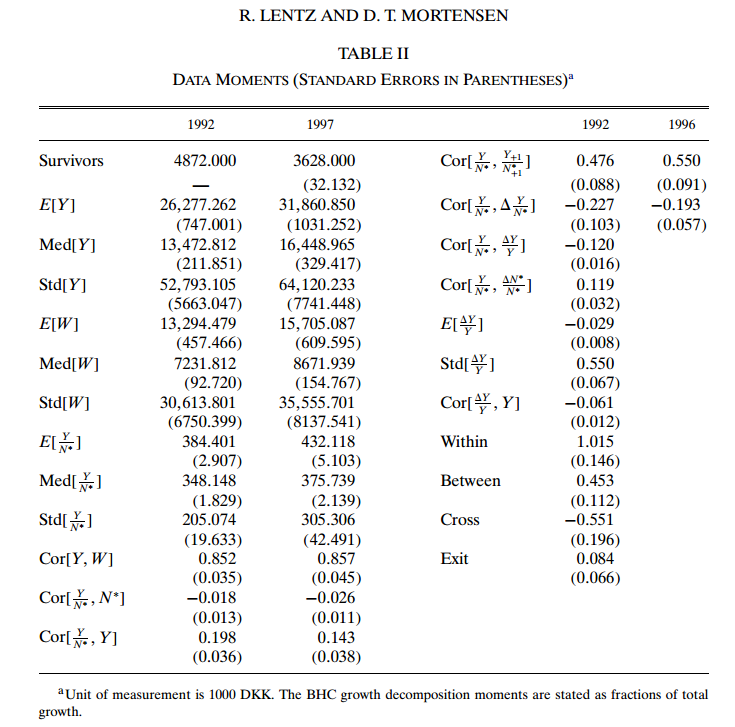
表Ⅱ的前两列用括号中的标准差表示一组分布矩。标准偏差是通过在原始面板上自抽样获得的。除非另有说明,金额均以丹麦统计局消费的1992年1000丹麦克朗为单位,并引入价格指数用于缩小名义数额。
规模分布的特征是明显的偏斜。每个员工的增加值分布显示出一定的偏差和显著的离散性。所有的分布图都出现了右移。分布矩还包括企业生产率与产出规模之间的正相关,以及企业生产率与劳动力规模之间的轻微负相关。
表Ⅱ的最后两列包含估计中使用的动态力矩。首先,请注意,经验性企业的生产力表现出显著的持久性和一些平均回归。动态矩还包括显示出显著离散度的增长率的横截面分布。此外,数据中产出大小与增长率之间存在轻微的负相关与公司增长率(△Y/Y)有关的时刻包括公司死亡,具体而言,一个退出的公司将有助于统计。由于企业规模与企业退出风险率之间存在负相关关系,因此,从增长统计数据中排除企业死亡会导致企业规模与增长之间存在更为显著的负相关关系。这是因为该模型还表现出退出率和规模之间的负相关,所以在模型模拟中也将是同样的情况。
最后,表Ⅱ还包括了一个标准的经验劳动生产率增长分解。作者选用了Foster,Haltiwanger和Krizan(2001)中使用的公式,该公式取自Baily,Bartelsman和Haltiwanger(1996),最终基于Baily,Hulten和Campbell(1992)index(BHC)。分解的形式为:


4.2 稳态下BHC的增长分解
基于BHC分解恒等式的研究为再分配作为总生产率增长来源的重要性提供了好坏参半的证据。根据美国制造业的数据,Bartelsman和Doms(2000)发现大约四分之一的增长可归因于总量再分配,另外四分之一归因于净进入,以及大约一半的增长归因于公司内部增长。然而,根据同样的数据,Foster,Haltiwanger和Krizan(2001)发现即使劳动份额保持在最初水平不变,劳动生产率的大部分增长也将发生。(经济合作与发展组织)对若干不同国家进行的一项研究中,Scarpetta,Hemmings,Tressel和Woo(2002)还发现,大部分增长可归因于公司内部的增长。
在这一部分,作者认为在文章模型中,公司之间(between)的组成部分没有捕捉到增长过程中再分配的作用。尽管在模型中,所有增长都与员工重新分配相关联,但该术语通常被解释为:总重新分配的贡献在我们的数据中接近于零。这是因为:尽管在该模型中,由于更频繁的创新,利润更高的公司平均增长更快,但根据定义,在该模型的各态历经稳态中,每种公司类型所提供的产品和所需投入的总份额是恒定的。因此,“between”和“cross”的术语在Foster,Haltiwanger和Krizan(2001)没有测量误差和暂时冲击的情况下,分解应当为零。


4.3 模型估计


4.4 模型细节说明与拟合


4.5 识别模拟结果



4.6 估计结果


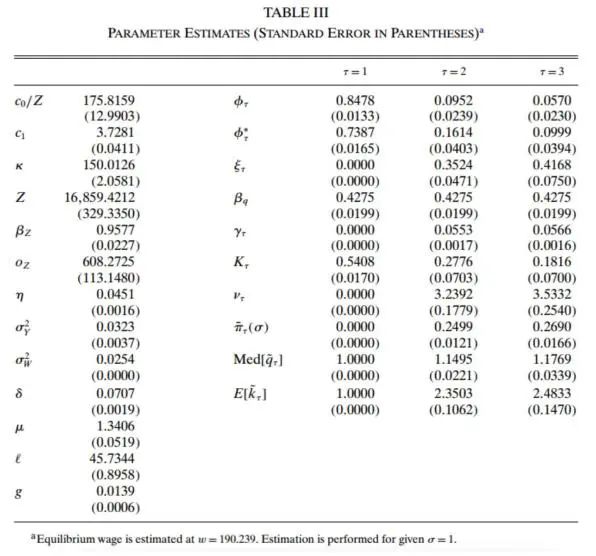


4.7 模型拟合
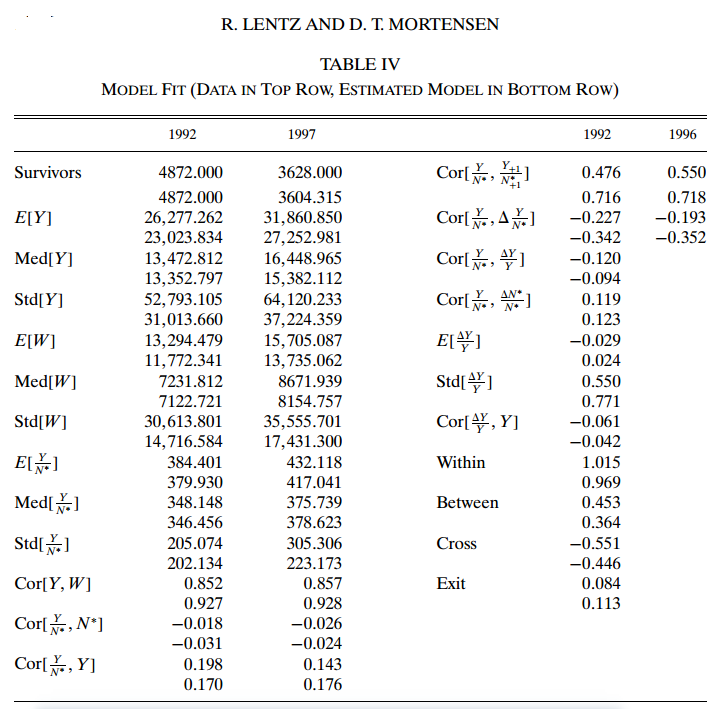
表Ⅳ显示了估计模型的数据矩和模拟矩的比较。模拟矩被计算为所有自助模拟的平均矩实现。
4.7.1 规模分布

4.7.2 生产力和规模的相关性
下图显示了数据和估计模型的经验企业生产力和规模的非参数回归。该模型在解释关系方面表现良好,至少在劳动生产率分布的中心部分是这样。
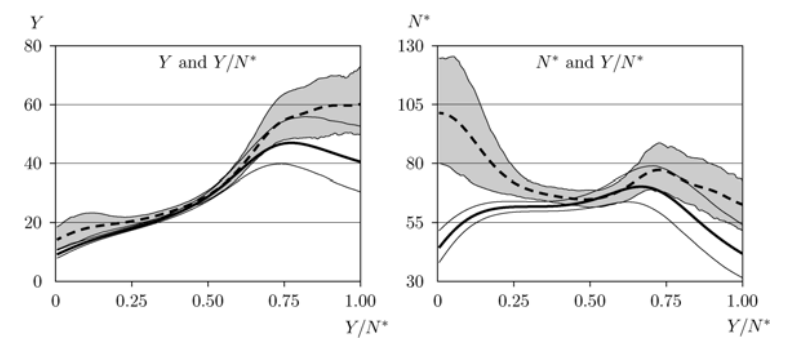
如前一节所述,企业类型的异质性在解释生产力和规模相关性方面起着重要的作用。在数据中,每个工人的增加值与产出规模之间的正相关关系表明,公司的工资份额与其增长率之间存在负相关关系。
4.7.3 每个工人的增加值分布
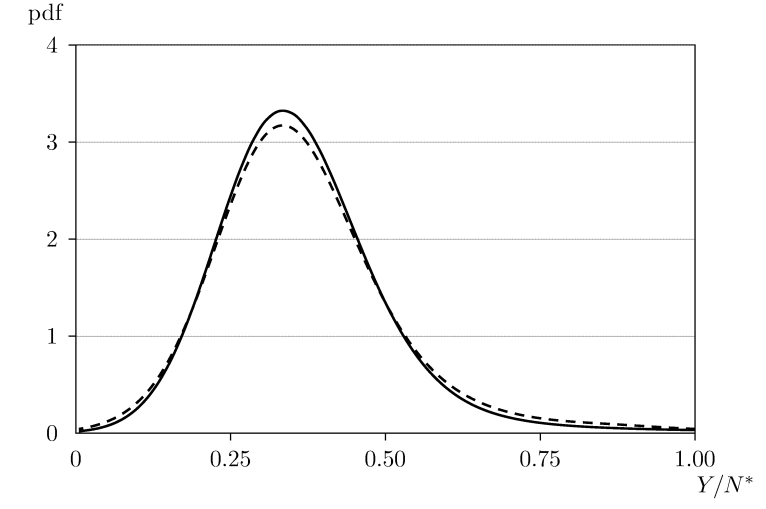

在缺乏创新劳动力需求的情况下,需求侧冲击对公司的增加值没有影响,因为制造业劳动力需求和增加值随着需求实现是成比例变化的。然而,需求侧冲击可以通过对制造和创新劳动力需求相对规模的影响来影响每个工人的增加值分散。如果除了零测量误差冲击外,还在没有需求实现离散的情况下估计模型,1992年的.Std[Y/N]估计几乎没有变化,这意味着需求实现离散对Y/N分布几乎没有影响。
4.7.4 从1992年到1997年的横断面变化

4.7.5 稳健的增长率分布和退出风险

4.7.6 每个工人的增加值持久性和均值回归


4.7.7 增长率和规模(Gibrat定律)
始于Gibrat(1931),很多人都强调企业增长和企业规模之间的内在关系人们试图用吉布拉特定律来暗示,一家公司的增长率与规模无关。然而,从图中可以看出,在当前的增长率-规模回归包括公司退出的公司样本中,仍然可以获得负相关。
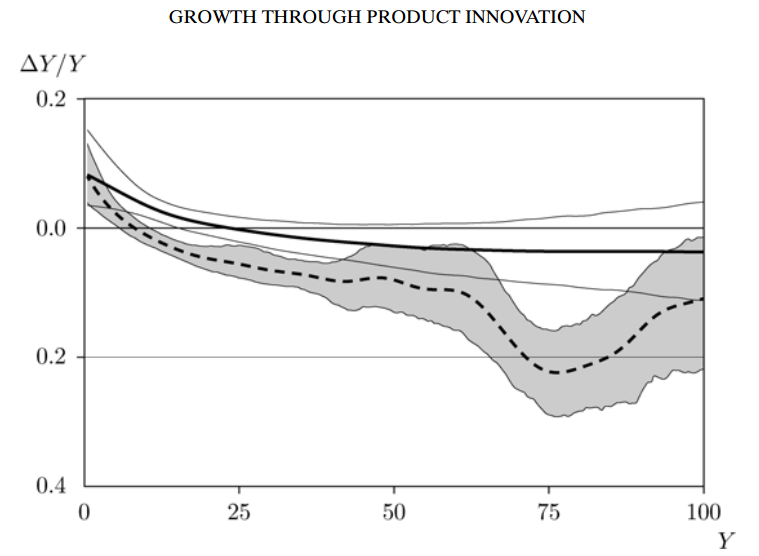
在理论层面,该模型满足Gibrat定律,即每个公司的预期增长与规模无关但两个相反的效应将影响无条件的规模和增长关系:第一,由于选择效应,较大的公司将倾向于过多呈现较高创造率类型,并且相对而言,选择效应将使得规模和无条件的公司增长率之间形成正关系。其次,需求冲击、计量误差以及(在较小程度上)供应冲击中的均值回归带来了相反的效果:如今的小公司群体往往会让处于负需求和计量误差冲击下的公司规模扩大。下一次创新带来的需求实现可能会逆转这些公司的命运,它们的增长率可能会相对较高。
4.7.6 福斯特–霍尔特万格–克里桑劳动生产率增长分解
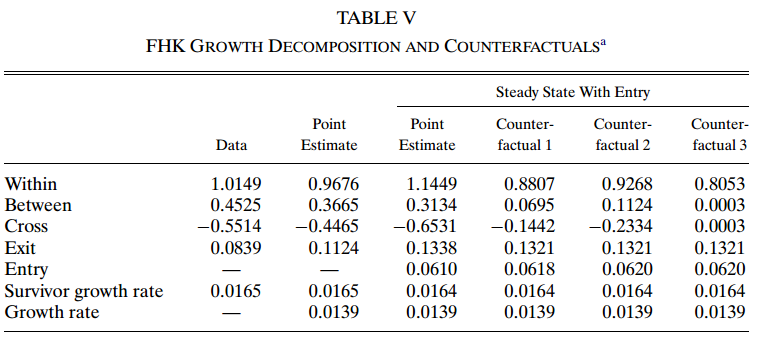
上表给出了分解结果。值得注意的是,每个工人的增加值增长的部分,都是幸存者选择偏差的结果(退出企业的工人自然不包含在内)。因此,该表列出了选定的幸存的1992年公司样本的增长指标和总体稳态增长率。在该模型结果中稳态年增长率为0.0139,而幸存选择样本的年增长率为0.0164。表中前两列的比较,表V表明所估计的模型相当好地拟合了BHC分解的情况。后三列基于反事实的噪声消除步骤。

05 | 工人再分配和增长
公式(31)中定义的总生产力增长是进入者和现有者贡献的总和,其中每项等于创新相对于被替代产品或服务的平均生产力的类型增--创新频率和质量改进的产物--加权反映在每种类型提供的产品线的比例中的相对规模。具体来说,由于不同公司所创造的产品的预期生产率是不同的,而且由于这些差异与预期盈利能力的差异呈正相关,因此,在创造率方面,总体增长反映了通过创造性破坏过程选择更有利可图的公司。实际上,公式(31)可以在σ=1的情况写为:

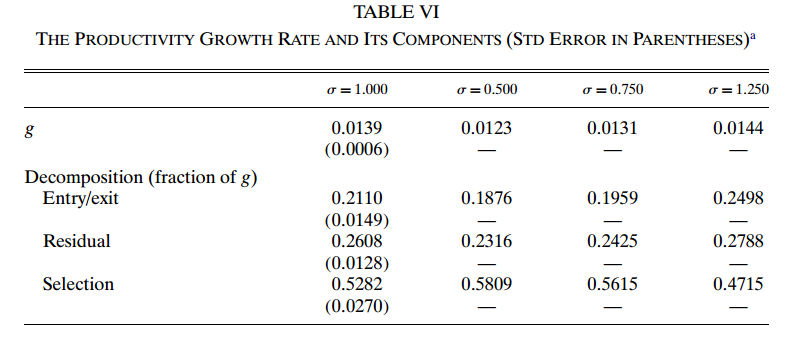
表Ⅵ给出了估计模型g=0.0139所隐含的平衡稳态年增长率。如表V所述,该样本的年增长率为0.0165。由于幸存者的选择,这个估计是向上的。传统的增长指标(TD指数)是0.0148。然而,在存在与稳定增长率呈负相关的出口风险异质性的情况下,TD指数也会向上倾斜。稳态增长率g=0.0139的模型估计提供了数据中样本选择偏差的结构调整。
表Ⅵ为分解估计值。估计的模型表明,进入/退出成分占21%,选择成分占53%,剩余成分占总增长率的26%。因此,进入和企业规模演变的动态过程个涉及不断重新分配到新的和不断增长的企业的过程,是模型经济增长的近四分之三的原因。该模型中的所有增长都是员工重新分配的结果。每当一个新的创新被创造出来,工人就会从拥有最近已经过时的产品的公司流向它的供应商。
06 | 总结与评价
企业生产率和企业规模之间存在巨大而持久的差异。异质性诱导的工人再分配应该是总生产率增长的一个重要来源。然而,基于Baily,Hulten和Campbell(1992)增长分解发现,重要性重新分配作为增长来源的证据好坏参半。我们认为,BHC增长分解没有正确识别资源再分配对生产率增长的稳态贡献。事实上,我们表明,其中跨公司类型的资源分布是平稳的模型暗示,在没有暂时噪声的情况下,分解的“between”和“cross”公司组成部分是零,无论真正的数据生成过程是什么。
在作者这个版本的模型中,通过创造性破坏的过程,能够开发出高质量产品的公司有一种动机,即相对于每一批利润较低的公司而言,能够增长得更快。这一过程导致工人从利润较低的公司重新分配到利润较高的公司,这有助于总生产率的增长。此外,该模型与以下观察结果一致:就业规模与劳动生产率之间没有相关性,而在丹麦公司数据中观察到的增加值与劳动生产率之间存在正相关性。总体创造和销毁率估计为年增长率δ=0.07,因此,产品的隐含平均寿命约为14年。
我们将该模型用于1992-1997年期间的丹麦公司数据。参数估计是合理的,并且该模型提供了与数据的接头尺寸分布和动态力矩的良好拟合。尽管该模型符合Foster,Haltiwanger,和Krizan(2001)作为BHC增长修正头寸的变体,在一次反事实操作中,介于和交叉项消失了,在该操作中,纯粹暂时性的冲击和测量误差被设置为零。最后,估计模型还拟合了数据中规模与增长之间的负关系,尽管在理论层面上,它满足Gibrat定律,即企业的创新率与其规模无关。
我们模型中的所有增长都归因于再分配,也就是说,再资源必须从失去市场的企业流向提供更有生产力的新产品和服务的创新者。
我们将再分配成分分解为来自企业进入和退出的净贡献、企业类型选择效应和剩余。进入的净贡献是模型隐含贡献的21%。选择部分占增长的53%,它抓住了以下事实的贡献:资源从增长缓慢的低生产力公司重新分配到快速增长的更有创造力的公司。
参考文献
[1]Foster, L., J. Haltiwanger, and C. Krizan (2001): “Aggregate Productivity Growth: Lessons From Microeconomic Evidence,” in New Developments in Productivity Analysis, ed. by C. R. Hulten, E. R. Dean, and M. J. Harper. Chicago : University of Chicago Press.
[2]Gibrat, R. (1931): Les Inégalités Économiques; Applications: Aux Inégalités des Richesses, À la Concentration des Entreprises, Aux Populations Des Villes, Aux Statistiques Des Familles, Etc. d' Une Loi Nouvelle, la Loi de l' Effet Proportionnel. Paris : Librairie du Recueil Sirey.
[3]Horowitz, J. L. (1998): “Bootstrap Methods for Covariance Structures,” Journal of Human Resources, 33, 39–61.
[4]Klette, T. J., and S. Kortum (2004): “Innovating Firms and Aggregate Innovation,” Journal of Political Economy, 112, 986–1018.
[5]Lentz, R., and D. T. Mortensen (2005): “Productivity Growth and Worker Reallocation,” International Economic Review, 46, 731–751.
文稿:杨惠晴 杨璐菱 曾艺孜
编辑:冯双婷
审校:何秋谷
2024年5月8日
